题目内容
11.下列说法中正确的是( )| A. | “f(0)=0”是“函数f(x)是奇函数”的充要条件 | |
| B. | 若p:?x0∈R,x02-x0-1>0,则¬p:?x∈R,x2-x-1<0 | |
| C. | 若p∧q为假命题,则p,q均为假命题 | |
| D. | “若$α=\frac{π}{6}$,则$sinα=\frac{1}{2}$”的逆否命题为真命题 |
分析 举例说明A错误;写出特称命题的否定说明B错误;由复合命题的真假判断说明C错误;由互为逆否命题的两个命题共真假说明D正确.
解答 解:对于函数f(x)=x2,有f(0)=0,函数f(x)为偶函数,函数f(x)=$\frac{1}{x}$为奇函数,但f(0)≠0.
∴“f(0)=0”是“函数f(x)是奇函数”的既不充分也不必要条件.A错误;
若p:?x0∈R,x02-x0-1>0,则¬p:?x∈R,x2-x-1≤0.B错误;
若p∧q为假命题,则p,q中至少一个为假命题.C错误;
由$α=\frac{π}{6}$,得$sinα=\frac{1}{2}$,∴命题“若$α=\frac{π}{6}$,则$sinα=\frac{1}{2}$”为真命题,其逆否命题为真命题.正确.
故选:D.
点评 本题考查命题的真假判断与应用,考查了命题的否定与逆否命题,训练了充分必要条件的判定方法,是基础题.

练习册系列答案
相关题目
6.命题p:?x>0,总有x2-1≥0,则?p为( )
| A. | ?x0≤0,使得x2-1<0 | B. | ?x0>0,使得x2-1<0 | ||
| C. | ?x>0,总有x2-1<0 | D. | ?x≤0,总有x2-1<0 |
1.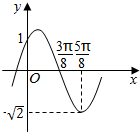 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ≤$\frac{π}{2}$)的图象如图所示,将f(x)的图象向左平移$\frac{π}{8}$个单位后得到函数g(x)的图象,则( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ≤$\frac{π}{2}$)的图象如图所示,将f(x)的图象向左平移$\frac{π}{8}$个单位后得到函数g(x)的图象,则( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ≤$\frac{π}{2}$)的图象如图所示,将f(x)的图象向左平移$\frac{π}{8}$个单位后得到函数g(x)的图象,则( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ≤$\frac{π}{2}$)的图象如图所示,将f(x)的图象向左平移$\frac{π}{8}$个单位后得到函数g(x)的图象,则( )| A. | g(x)=$\sqrt{2}$sin(2x+$\frac{3π}{8}$) | B. | g(x)=$\sqrt{2}$cos2x | C. | g(x)=$\sqrt{2}$cos(2x+$\frac{3π}{8}$) | D. | g(x)=$\sqrt{2}$sin2x |
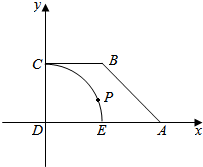 已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.
已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.