题目内容
19.对定义在[0,1]上的函数f(x),如果同时满足以下三个条件:①对任意x∈[0,1],总有f(x)≥0;
②f(1)=1;
③若x1≥0,x2≥0,x1+x2≤1,有f(x1+x2)≥f(x1)+f(x2)成立.
则称函数f(x)为理想函数.
(1)判断g(x)=2x-1(x∈[0,1])是否为理想函数,并说明理由;
(2)若f(x)为理想函数,求f(x)的最小值和最大值;
(3)若f(x)为理想函数,假设存在x0∈[0,1]满足f[f(x0)]=x0,求证:f(x0)=x0.
分析 (1)①要判断函数g(x)=2x-1,(x∈[0,1])在区间[0,1]上是否为“理想函数,只要检验函数g(x)=2x-1,是否满足理想函数的三个条件即可;
(2)先研究函数f(x)的单调性,从而得出此函数的最值.得到当x=0时,f(x)取得最小值2,当x=1时,f(x)取得最大值3即可;
(3)由条件③知,任给m、n∈[0,1],当m<n时,由m<n知n-m∈[0,1],f(n)=f(n-m+m)≥f(n-m)+f(m)≥f(m).由此能够推导出f(x0)=x0.,根据f[f(x0)]=x0,则f(x0)=x0.
解答 解:(1)①显然f(x)=2x-1在[0,1]上满足f(x)≥0;②f(1)=1.
若x1≥0,x2≥0,且x1+x2≤1,
则有f(x1+x2)-[f(x1)+f(x2)]=2x1+x2-1-[(2x1-1)+(2x2-1)]=(2x2-1)(2x1-1)≥0
故f(x)=2x-1满足条件①②③,所以f(x)=2x-1为理想函数,
(2)设x1,x2∈[0,1],x1<x2,则x2-x1∈(0,1]
∴f(x2)=f[(x2-x1)+x1]≥f(x2-x1)+f(x1)-2
∴f(x2)-f(x1)≥f (x2-x1)-2≥0,
∴f(x1)≤f(x2),则当0≤x≤1时,f(0)≤f(x)≤f(1),
在③中,令x1=x2=0,得f(0)≤2,由②得f(0)≥2,
∴f(0)=2当x=1时,f(1)=3,
∴当x=0时,f(x)取得最小值2,
当x=1时,f(x)取得最大值3,
(3)由条件③知,任给m、n∈[0,1],当m<n时,由m<n知n-m∈[0,1],
∴f(n)=f(n-m+m)≥f(n-m)+f(m)≥f(m).
若f(x0)>x0,则f(x0)≤f[f(x0)]=x0,前后矛盾;
若:f(x0)<x0,则f(x0)≥f[f(x0)]=x0,前后矛盾.
故f(x0)=x0.
点评 赋值法是解决抽象函数问题的常用方法,函数的新定义则转化为函数性质问题,本题则结合指数函数的性质,探讨函数的函数值域,指数函数的单调性的应用等知识点.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
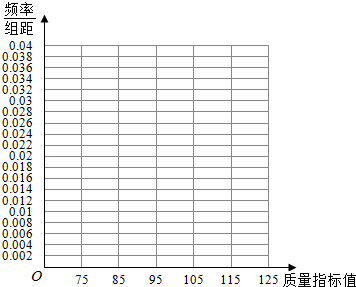
小夫子全能检测系列答案| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
(Ⅱ)估计这种产品质量指标值的众数、中位数及平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
| A. | $\frac{1}{7}$ | B. | $-\frac{1}{7}$ | C. | -7 | D. | 7 |
| A. | “f(0)=0”是“函数f(x)是奇函数”的充要条件 | |
| B. | 若p:?x0∈R,x02-x0-1>0,则¬p:?x∈R,x2-x-1<0 | |
| C. | 若p∧q为假命题,则p,q均为假命题 | |
| D. | “若$α=\frac{π}{6}$,则$sinα=\frac{1}{2}$”的逆否命题为真命题 |