题目内容
1.设变量x,y满足约束条件:$\left\{\begin{array}{l}{x+y≥3}\\{x-y≥-1}\\{2x-y≤3}\end{array}\right.$,则$\frac{y}{x}$的取值范围为[$\frac{1}{2},2$].分析 由约束条件作出可行域,然后利用$\frac{y}{x}$的几何意义结合两点求斜率得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y≥3}\\{x-y≥-1}\\{2x-y≤3}\end{array}\right.$作出可行域如图,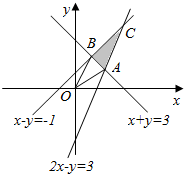
联立$\left\{\begin{array}{l}{x+y=3}\\{2x-y=3}\end{array}\right.$,解得A(2,1),
联立$\left\{\begin{array}{l}{x-y=-1}\\{x+y=3}\end{array}\right.$,解得B(1,2),
∵${k}_{OA}=\frac{1}{2},{k}_{OB}=2$.
∴$\frac{y}{x}$的取值范围为[$\frac{1}{2},2$].
故答案为:[$\frac{1}{2},2$].
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,考查数学转化思想方法,是中档题.

练习册系列答案
相关题目
11.已知角α的终边上有一点P(1,3),则$\frac{sin(π-α)-sin(\frac{π}{2}+α)}{cos(\frac{3π}{2}-α)+2cos(-π+α)}$的值为( )
| A. | -$\frac{2}{5}$ | B. | -$\frac{4}{5}$ | C. | -$\frac{4}{7}$ | D. | -4 |
12.已知下表中的对数值有且只有一个是错误的.
其中错误的对数值是lg1.5.
| x | 1.5 | 3 | 5 | 6 | 8 | 9 |
| lg x | 4a-2b+c | 2a-b | a+c | 1+a-b-c | 3[1-(a+c)] | 2(2a-b) |