题目内容
10.如果函数f(x)对其定义域内的任意两个实数x1,x2都满足不等式f($\frac{{x}_{1}+{x}_{2}}{2}$)<$\frac{f({x}_{1})+f({x}_{2})}{2}$,则称函数f(x)在定义域上具有性质M,给出下列函数:①y=$\sqrt{x}$;②y=x2;③y=2x;④y=log2x.其中具有性质M的是②③(填上所有正确答案的序号)
分析 由不等式f($\frac{{x}_{1}+{x}_{2}}{2}$)<$\frac{f({x}_{1})+f({x}_{2})}{2}$,可知:函数为下凸函数,画出图象即可判断出.
解答 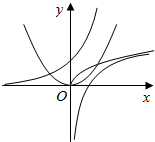 解:函数f(x)对其定义域内的任意两个实数x1,x2都满足不等式f($\frac{{x}_{1}+{x}_{2}}{2}$)<$\frac{f({x}_{1})+f({x}_{2})}{2}$,则称函数f(x)在定义域上具有性质M,(为下凸函数).
解:函数f(x)对其定义域内的任意两个实数x1,x2都满足不等式f($\frac{{x}_{1}+{x}_{2}}{2}$)<$\frac{f({x}_{1})+f({x}_{2})}{2}$,则称函数f(x)在定义域上具有性质M,(为下凸函数).
由函数的图象可知:②y=x2;③y=2x.其中具有性质M.
故答案为:②③.
点评 本题考查了下凸函数的性质,考查了数形结合思想方法与推理能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.在锐角三角形ABC中,角A,B所对的边分别为a,b,若2asinB=b,则角A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{12}$ | D. | $\frac{π}{3}$ |
18.若f(sinx)=cos2x,那么f(cosx)等于( )
| A. | sin2x | B. | cos2x | C. | -sin2x | D. | -cos2x |