题目内容
【题目】已知等比数列{an}满足a1=2,a2=4(a3﹣a4),数列{bn}满足bn=3﹣2log2an .
(1)求数列{an},{bn}的通项公式;
(2)令cn= ![]() ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn;
(3)若λ>0,求对所有的正整数n都有2λ2﹣kλ+2>a2nbn成立的k的取值范围.
【答案】
(1)解:设等比数列{an}的公比为q,∵a1=2,a2=4(a3﹣a4),
∴a2=4a2(q﹣q2),化为:4q2﹣4q+1=0,解得q= ![]() .
.
∴an= ![]() =22﹣n.
=22﹣n.
∴bn=3﹣2log2an=3﹣2(2﹣n)=2n﹣1
(2)解:cn= ![]() =
= ![]() =
= ![]() .
.
∴数列{cn}的前n项和Sn= ![]() [2+322+5×23+…+(2n﹣1)2n],
[2+322+5×23+…+(2n﹣1)2n],
∴2Sn= ![]() [22+323+…+(2n﹣3)2n+(2n﹣1)2n+1],
[22+323+…+(2n﹣3)2n+(2n﹣1)2n+1],
∴﹣Sn= ![]() =
=  ,
,
可得:Sn= ![]()
(3)解:不等式2λ2﹣kλ+2>a2nbn,即2λ2﹣kλ+2>22﹣2n(2n﹣1),
令dn=22﹣2n(2n﹣1),则dn+1﹣dn= ![]() ﹣
﹣ ![]() =
= ![]() =
= ![]() <0,
<0,
因此dn+1<dn,即数列{dn}单调递减,因此n=1时dn取得最大值d1=1.
∵对所有的正整数n都有2λ2﹣kλ+2>a2nbn成立,
∴2λ2﹣kλ+2>1,∵λ>0.
∴k<2 ![]() ,∵2
,∵2 ![]() ≥2
≥2 ![]() =2
=2 ![]() ,当且仅当λ=
,当且仅当λ= ![]() 时取等号.
时取等号.
∴ ![]() .
.
即k的取值范围是 ![]()
【解析】(1)设等比数列{an}的公比为q,根据a1=2,a2=4(a3﹣a4),可得a2=4a2(q﹣q2),化简解得q.可得an.利用对数的运算性质可得bn.(2)cn= ![]() =
= ![]() =
= ![]() .利用错位相减法与等比数列的求和公式即可得出.(3)不等式2λ2﹣kλ+2>a2nbn,即2λ2﹣kλ+2>22﹣2n(2n﹣1),令dn=22﹣2n(2n﹣1),通过作差可得:dn+1<dn,即数列{dn}单调递减,因此n=1时dn取得最大值d1=1.根据对所有的正整数n都有2λ2﹣kλ+2>a2nbn成立,可得2λ2﹣kλ+2>1,根据λ>0.可得k<2
.利用错位相减法与等比数列的求和公式即可得出.(3)不等式2λ2﹣kλ+2>a2nbn,即2λ2﹣kλ+2>22﹣2n(2n﹣1),令dn=22﹣2n(2n﹣1),通过作差可得:dn+1<dn,即数列{dn}单调递减,因此n=1时dn取得最大值d1=1.根据对所有的正整数n都有2λ2﹣kλ+2>a2nbn成立,可得2λ2﹣kλ+2>1,根据λ>0.可得k<2 ![]() ,再利用基本不等式的性质即可得出.
,再利用基本不等式的性质即可得出.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系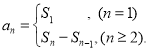 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案