题目内容
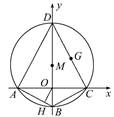
如图,椭圆C0: (a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a.点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.
(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a.点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.

(1)求直线AA1与直线A2B交点M的轨迹方程;
(2)设动圆C2:x2+y2=t22与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:t12+t22为定值.
 (a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a.点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.
(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a.点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.
(1)求直线AA1与直线A2B交点M的轨迹方程;
(2)设动圆C2:x2+y2=t22与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:t12+t22为定值.
(1)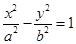 (x<-a,y<0) (2)见解析
(x<-a,y<0) (2)见解析
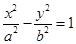 (x<-a,y<0) (2)见解析
(x<-a,y<0) (2)见解析(1)解 设A(x1,y1),B(x1,-y1),
又知A1(-a,0),A2(a,0),
则直线A1A的方程为y=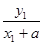 (x+a),①
(x+a),①
直线A2B的方程为y=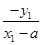 (x-a).②
(x-a).②
由①②得y2=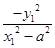 (x2-a2).③
(x2-a2).③
由点A(x1,y1)在椭圆C0上,故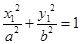 .
.
从而y12=b2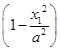 ,
,
代入③得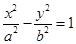 (x<-a,y<0).
(x<-a,y<0).
(2)证明 设A′(x2,y2),由矩形ABCD与矩形A′B′C′D′的面积相等,得4|x1||y1|=4|x2||y2|,
故x12y12=x22y22.
因为点A,A′均在椭圆上,
所以b2x12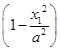 =b2x22
=b2x22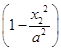 .
.
由t1≠t2,知x1≠x2,所以x12+x22=a2.从而y12+y22=b2,
因此t12+t22=a2+b2为定值.
又知A1(-a,0),A2(a,0),
则直线A1A的方程为y=
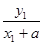 (x+a),①
(x+a),①直线A2B的方程为y=
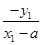 (x-a).②
(x-a).②由①②得y2=
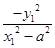 (x2-a2).③
(x2-a2).③由点A(x1,y1)在椭圆C0上,故
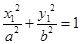 .
.从而y12=b2
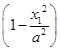 ,
,代入③得
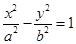 (x<-a,y<0).
(x<-a,y<0).(2)证明 设A′(x2,y2),由矩形ABCD与矩形A′B′C′D′的面积相等,得4|x1||y1|=4|x2||y2|,
故x12y12=x22y22.
因为点A,A′均在椭圆上,
所以b2x12
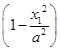 =b2x22
=b2x22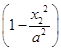 .
.由t1≠t2,知x1≠x2,所以x12+x22=a2.从而y12+y22=b2,
因此t12+t22=a2+b2为定值.

练习册系列答案
相关题目
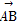 ·
·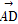 =0,求D2+E2-4F的值.
=0,求D2+E2-4F的值.
 上,求圆C的方程。
上,求圆C的方程。 其中
其中 ,当
,当 ,
, 变化时,则满足条件的点
变化时,则满足条件的点 在平面上所组成图形的面积是( )
在平面上所组成图形的面积是( )
 (
(

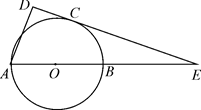
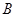 是斜边AE的中点,以
是斜边AE的中点,以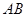 为直径的圆O与边DE相切于点C,若AB=3,则线段CD的长为.
为直径的圆O与边DE相切于点C,若AB=3,则线段CD的长为.