题目内容
已知|AB|＝2，动点P满足|PA|＝2|PB|，试建立恰当的直角坐标系，动点P的轨迹方程为________．
(x－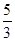
)2＋y2＝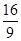
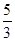)2＋y2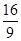＝如图所示，以AB的中点O为原点，直线AB为x轴建立直角坐标系，则A(－1,0)，B(1,0)．
设P(x，y)，因为|PA|＝2|PB|，所以
＝2
.
两边平方，得(x＋1)2＋y2＝4[(x－1)2＋y2]．
整理，得x2＋y2－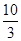
x＋1＝0，即(x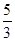－)2＋y2＝.
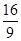故动点P的轨迹方程为(x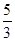－)2＋y2＝.
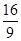设P(x，y)，因为|PA|＝2|PB|，所以
＝2.两边平方，得(x＋1)2＋y2＝4[(x－1)2＋y2]．
整理，得x2＋y2－
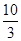x＋1＝0，即(x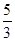－)2＋y2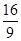＝.故动点P的轨迹方程为(x－
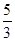)2＋y2＝.
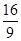练习册系列答案
相关题目
是圆
的直径，
是圆
(a＞b＞0，a，b为常数)，动圆C1：x2＋y2＝t12，b＜t1＜a．点A1，A2分别为C0的左，右顶点，C1与C0相交于A，B，C，D四点．
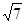，求圆C方程．
是圆
外一点，过
．
的两条直角边AC，BC的长分别为3cm，4cm，以AC为直径作圆与斜边AB交于点D，则BD的长为 ；