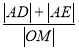题目内容
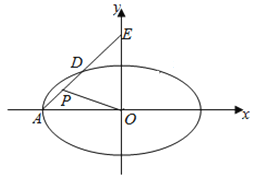
【题目】已知椭圆![]() :
:![]() ,动直线l与椭圆E交于不同的两点
,动直线l与椭圆E交于不同的两点![]() ,
,![]() ,且△AOB的面积为1,其中O为坐标原点.
,且△AOB的面积为1,其中O为坐标原点.
(1)证明:![]() 为定值;
为定值;
(2)设线段AB的中点为M,求![]() 的最大值.
的最大值.
【答案】(1)证明见解析;(2)最大值为![]() .
.
【解析】
(1)当直线l的斜率不存在时,设l:x=m,代入椭圆方程求解![]() ,结合△AOB的面积为1求得m值,可得
,结合△AOB的面积为1求得m值,可得![]() 为定值4,当直线l的斜率存在时,设
为定值4,当直线l的斜率存在时,设![]() ,联立椭圆方程,可得A,B横坐标的和与积,利用弦长公式求弦长,再由点到直线的距离公式求得
,联立椭圆方程,可得A,B横坐标的和与积,利用弦长公式求弦长,再由点到直线的距离公式求得![]() 到直线
到直线![]() 的距离,结合△AOB的面积为1,可得
的距离,结合△AOB的面积为1,可得![]() ,则
,则![]() 的值可求,从而说明
的值可求,从而说明![]() 为定值;
为定值;
(2)设![]() ,当直线的斜率不存在时,
,当直线的斜率不存在时,![]() ,
,![]() ,则|
,则|![]() ;当直线的斜率存在时,由(1)可得M的坐标,求得
;当直线的斜率存在时,由(1)可得M的坐标,求得![]() ,写出
,写出![]() ,结合
,结合![]() 转化为关于
转化为关于![]() 的二次函数求最值.
的二次函数求最值.
(1)当直线l的斜率不存在,设l:x=m
代入椭圆方程,得![]() ,即
,即![]()
由△AOB的面积为1,可得![]() ,
,
解得:![]() ,则
,则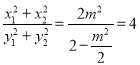 ;
;
当直线l的斜率存在,设![]() ,
,
联立 ,
,
化简整理可得![]() ,
,
设![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,
![]()
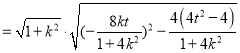
![]() ,
,
由△AOB的面积为1,可得![]() ,
,
化简可得![]() ,
,
则![]()
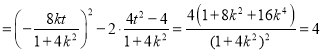 ,
,
而 ,
,
综上可得,![]() 为定值4;
为定值4;
(2)设![]() ,
,
当直线的斜率不存在时,![]() ,
,
![]() ,则|
,则|![]() ;
;
当直线的斜率存在时,由(1)可得![]() ,
,
![]() ,
,
则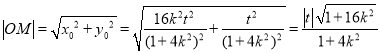 ,
,
可得![]()
![]() .
.
∵![]() ,∴
,∴![]() .
.
可知![]() .
.
综上,![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
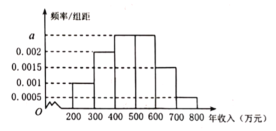
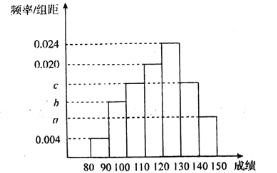
【题目】高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:![]()
![]()
![]()
![]()
![]()
![]()
![]() .其中a,b,c成等差数列且
.其中a,b,c成等差数列且![]() .物理成绩统计如表.(说明:数学满分150分,物理满分100分)
.物理成绩统计如表.(说明:数学满分150分,物理满分100分)
分组 |
|
|
|
|
|
频数 | 6 | 9 | 20 | 10 | 5 |
(1)根据频率分布直方图,请估计数学成绩的平均分;
(2)根据物理成绩统计表,请估计物理成绩的中位数;
(3)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知本班中至少有一个“优”同学总数为6人,从此6人中随机抽取3人,记X为抽到两个“优”的学生人数,求X的分布列和期望值.