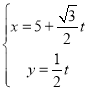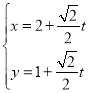题目内容
【题目】已知函数![]() ,下列说法正确的是__________.
,下列说法正确的是__________.![]() 的值域是
的值域是![]() ;
;![]() 当
当![]() 时,方程
时,方程![]() 有两个不等实根;
有两个不等实根;![]() 若函数
若函数![]() 有三个零点时,则
有三个零点时,则![]() ;
;![]() 经过
经过![]() 有三条直线与
有三条直线与![]() 相切.
相切.
【答案】①②③
【解析】
①:结合导数,用函数的单调性和奇偶性,求得![]() 的值域;②利用导数,证得方程
的值域;②利用导数,证得方程![]() 有两个不等实根;③根据
有两个不等实根;③根据![]() 为偶函数,故可先考虑
为偶函数,故可先考虑![]() 的情况,再由对称性得到
的情况,再由对称性得到![]() 的情况.当
的情况.当![]() 时,首先确定
时,首先确定![]() 是函数
是函数![]() 的零点,令
的零点,令![]() ,分离常数
,分离常数![]() ,利用导数求得
,利用导数求得![]() 的取值范围.再根据对称性,求得
的取值范围.再根据对称性,求得![]() 的取值范围.④利用导数,求得过
的取值范围.④利用导数,求得过![]() 的切线的条数.
的切线的条数.
①函数![]() 的定义域为
的定义域为![]() ,且
,且![]() ,所以
,所以![]() 为偶函数,图像关于
为偶函数,图像关于![]() 轴对称.当
轴对称.当![]() 时,
时,![]() ,
,![]() ,
,![]() .令
.令![]() 解得
解得![]() ,所以
,所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,![]()
![]() ,所以
,所以![]() 在
在![]() 上单调递增,从而
上单调递增,从而![]() .由于
.由于![]() 为偶函数,所以
为偶函数,所以![]() 在
在![]() 上单调递减,且
上单调递减,且![]() .所以
.所以![]() 的值域是
的值域是![]() .故①正确.
.故①正确.
②显然,![]() 是方程
是方程![]() 的根.方程
的根.方程![]() 可化为
可化为![]() .当
.当![]() 时,即
时,即![]() .根据①的分析,结合图像可知,当
.根据①的分析,结合图像可知,当![]() 时
时![]() 与
与![]() 的图像没有公共点.故只需考虑
的图像没有公共点.故只需考虑![]() 的情况.由
的情况.由![]() 得
得![]() ,即
,即![]() .构造函数
.构造函数![]() ,
,![]() ,
,![]() ,令
,令![]() ,解得
,解得![]() .所以
.所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,且
上递增,且![]() ,所以存在
,所以存在![]() ,使得
,使得![]() .故
.故![]() 在
在![]() 上递减,在
上递减,在![]() 上递增.
上递增.![]() ,所以存在
,所以存在![]() ,使
,使![]() .综上所述,当
.综上所述,当![]() 时,方程
时,方程![]() 有两个不等实根成立,故②正确.
有两个不等实根成立,故②正确.
③![]() 为偶函数,故可先考虑
为偶函数,故可先考虑![]() 的情况.当
的情况.当![]() 时,函数
时,函数![]() 为
为![]() ,故方程
,故方程![]() 有三个不相等的实数根.首先
有三个不相等的实数根.首先![]() 是方程
是方程![]() 的根.
的根.
先证![]() :令
:令![]() ,
,![]() ,
,![]() ,令
,令![]() 解得
解得![]() .所以
.所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增.
上递增.![]() ,当
,当![]() ,
,![]() .若
.若![]() ,即
,即![]() ,则
,则![]() 在区间
在区间![]() 上先减后增,在区间
上先减后增,在区间![]() 上至多只有两个零点,不符合题意.故
上至多只有两个零点,不符合题意.故![]() .
.
故下证![]() :当
:当![]() 时,由
时,由![]() 得
得![]() 有两个不同的实数根.构造函数
有两个不同的实数根.构造函数![]() ,
,![]() .令
.令![]() ,
,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,
时,![]() .所以由
.所以由![]() 可知
可知![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,所以
上递增,所以![]() 在
在![]() 处取得极小值也即是最小值
处取得极小值也即是最小值![]() ,所以
,所以![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() .由于
.由于![]() 为偶函数,根据函数图像的对称性可知
为偶函数,根据函数图像的对称性可知![]() 的取值范围是
的取值范围是![]() .故③正确.
.故③正确.
④当![]() 时,设经过点
时,设经过点![]() 的切线的切点为
的切线的切点为![]() ,
,![]() ,
,![]() ,故切线方程为
,故切线方程为![]() ,将
,将![]() 代入上式得
代入上式得![]() ,化简得
,化简得![]() .令
.令![]() ,
,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递增.所以方程
上单调递增.所以方程![]() 解得
解得![]() 或
或![]() .所以当
.所以当![]() 时,
时,![]() 有两条切线.根据
有两条切线.根据![]() 为偶函数,所以当
为偶函数,所以当![]() 时,
时,![]() 也有两条切线方程. 所以经过
也有两条切线方程. 所以经过![]() 有四条直线与
有四条直线与![]() 相切,④错误.
相切,④错误.
特别的,当![]() 时,
时,![]() ,
,![]() ,即当
,即当![]() 时,
时,![]() 在
在![]() 处的切线的斜率为
处的切线的斜率为![]() .当
.当![]() 时,
时,![]() ,即当
,即当![]() 时,
时,![]() 在
在![]() 处的切线的斜率为
处的切线的斜率为![]() .
.
故答案为:①②③

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案