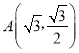题目内容
【题目】设数列![]() 的前
的前![]() 项和
项和![]() ,已知
,已知![]() ,
,![]() .
.
(1)求证:数列![]() 为等差数列,并求出其通项公式;
为等差数列,并求出其通项公式;
(2)设![]() ,又
,又![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() 为正整数且
为正整数且![]() ,数列
,数列![]() 共有
共有![]() 项,设
项,设![]() ,又
,又![]() ,求
,求![]() 的所有可能取值.
的所有可能取值.
【答案】(1)证明见解析;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
【解析】
(1)当![]() 时,由所给的递推关系式进行作差变形证明后项与前项之差为常数即可证得数列为等差数列,进一步可得数列的通项公式;
时,由所给的递推关系式进行作差变形证明后项与前项之差为常数即可证得数列为等差数列,进一步可得数列的通项公式;
(2)结合(1)中的通项公式裂项求和,然后结合题意可确定实数![]() 的取值范围;
的取值范围;
(3)首先确定数列![]() 为等差数列,然后结合数列的单调性确定绝对值符号进行求和,得到关于k的不等式,最后求解关于k的不等式即可确定实数
为等差数列,然后结合数列的单调性确定绝对值符号进行求和,得到关于k的不等式,最后求解关于k的不等式即可确定实数![]() 的所有可能取值.
的所有可能取值.
(1)当![]() 时,
时,![]() ,
,![]() ,
,
两式作差得![]() ,
,
故![]() ,
,
所以数列![]() 是公差为6的等差数列,
是公差为6的等差数列,
又![]() ,
,
所以![]() ;
;
(2)由于![]() ,故
,故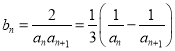 .
.
 ,
,
显然![]() 单调递增,且
单调递增,且![]() ,
,
故![]() , 所以
, 所以![]() .
.
(3)![]() ,则
,则![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,
故当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
设数列![]() 的前n项和为
的前n项和为![]() ,于是:
,于是:
![]()
![]() ,
,
注意到![]() ,则
,则![]() ,题中的不等式即
,题中的不等式即![]() ,
,
所以![]() ,
,
所以,![]() 的所有可取值为
的所有可取值为![]() .
.

练习册系列答案
相关题目