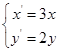题目内容
已知 ,
, ,
, ,映射
,映射 .对于直线
.对于直线 上任意一点
上任意一点 ,
, ,若
,若 ,我们就称
,我们就称 为直线
为直线 的“相关映射”,
的“相关映射”, 称为映射
称为映射 的“相关直线”.又知
的“相关直线”.又知
 ,则映射
,则映射 的“相关直线”有多少条( )
的“相关直线”有多少条( )
 ,
, ,
, ,映射
,映射 .对于直线
.对于直线 上任意一点
上任意一点 ,
, ,若
,若 ,我们就称
,我们就称 为直线
为直线 的“相关映射”,
的“相关映射”, 称为映射
称为映射 的“相关直线”.又知
的“相关直线”.又知
 ,则映射
,则映射 的“相关直线”有多少条( )
的“相关直线”有多少条( )A. | B. | C. | D.无数 |
B
试题分析:当直线
 的斜率存在时,不放设直线
的斜率存在时,不放设直线 的方程为
的方程为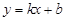 ,
,设点
 的坐标为
的坐标为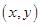 ,且
,且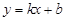 ,则点
,则点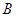 的坐标为
的坐标为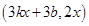 ,
,由于点
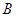 在直线
在直线 上,则有
上,则有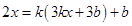 ,即
,即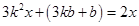 ,
,因此有
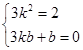 ,解得
,解得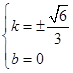 ;
;当直线
 的斜率不存在时,设直线
的斜率不存在时,设直线 的方程为
的方程为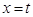 ,在此直线上任取一点
,在此直线上任取一点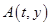 ,则点
,则点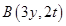 ,
,由于点
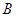 也在直线
也在直线 上,因此有
上,因此有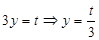 (非定值),此时,直线
(非定值),此时,直线 不存在.
不存在.综上所述,映射
 的“相关直线”为
的“相关直线”为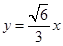 或
或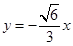 ,有两条,故选B.
,有两条,故选B.
练习册系列答案
相关题目
 .
. ,
, 时,若不等式
时,若不等式 恒成立,求
恒成立,求 的范围;
的范围; 在
在 内存在零点.
内存在零点.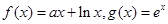 .
.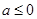 时,求
时,求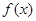 的单调区间;
的单调区间;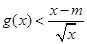 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;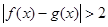 .
.
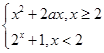 若f(f(1))>3a2,则a的取值范围是________.
若f(f(1))>3a2,则a的取值范围是________. ,若不等式
,若不等式 成立,则实数a的取值范围是( ).
成立,则实数a的取值范围是( ). }
} }
} }
} }
}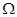 为平面直角坐标系
为平面直角坐标系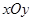 中的点集,从
中的点集,从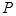 作
作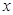 轴、
轴、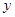 轴的垂线,垂足分别为
轴的垂线,垂足分别为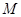 ,
,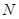 ,记点
,记点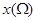 ,点
,点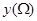 . 若
. 若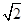 ;
;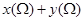 的取值范围是
的取值范围是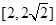 ;
;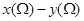 恒等于0.其中所有正确结论的序号是( )
恒等于0.其中所有正确结论的序号是( )