题目内容
某种新药服用x小时后血液中的残留量为y毫克,如图所示为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )


| A.上午10:00 | B.中午12:00 |
| C.下午4:00 | D.下午6:00 |
C
当x∈[0,4]时,设y=k1x,
把(4,320)代入,得k1=80,∴y=80x.
当x∈[4,20]时,设y=k2x+b.
把(4,320),(20,0)代入得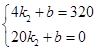
解得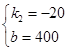
∴y=400-20x.
∴y=f(x)=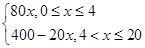
由y≥240,
得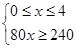 或
或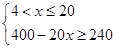
解得3≤x≤4或4<x≤8,
∴3≤x≤8.
故第二次服药最迟应在当日下午4:00.故选C.
把(4,320)代入,得k1=80,∴y=80x.
当x∈[4,20]时,设y=k2x+b.
把(4,320),(20,0)代入得
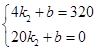
解得
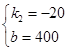
∴y=400-20x.
∴y=f(x)=
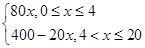
由y≥240,
得
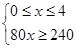 或
或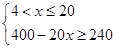
解得3≤x≤4或4<x≤8,
∴3≤x≤8.
故第二次服药最迟应在当日下午4:00.故选C.

练习册系列答案
相关题目
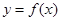 (
(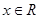 )的图象如图所示,则不等式
)的图象如图所示,则不等式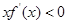 的解集为________.
的解集为________.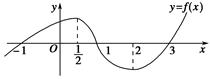
 、
、 满足
满足 ,则称
,则称 上的一组正交函数,给出三组函数:①
上的一组正交函数,给出三组函数:① ;②
;② ;③
;③ .
.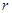 米,高为
米,高为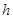 米,体积为
米,体积为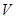 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为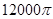 元(
元(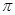 为圆周率).
为圆周率).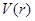 ,并求该函数的定义域;
,并求该函数的定义域; (a+b-|a-b|),如果函数f(x)=-x2+2x+3,g(x)=x+1,那么函数G(x)=F(f(x),g(x))的最大值等于________.
(a+b-|a-b|),如果函数f(x)=-x2+2x+3,g(x)=x+1,那么函数G(x)=F(f(x),g(x))的最大值等于________. ,
, ,
, ,映射
,映射 .对于直线
.对于直线 上任意一点
上任意一点 ,
, ,若
,若 ,我们就称
,我们就称 为直线
为直线
 ,则映射
,则映射


 的图象可能是( )
的图象可能是( )