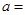题目内容
(本题满分14分)本题共有2个小题,第1小题满分6分,第2个小题满分8分。
已知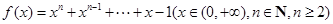 .
.
(1)当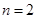 ,
, 时,若不等式
时,若不等式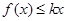 恒成立,求
恒成立,求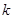 的范围;
的范围;
(2)试证函数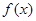 在
在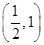 内存在零点.
内存在零点.
已知
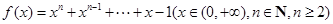 .
.(1)当
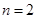 ,
, 时,若不等式
时,若不等式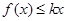 恒成立,求
恒成立,求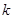 的范围;
的范围;(2)试证函数
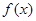 在
在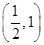 内存在零点.
内存在零点.(1)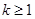 ,(2)详见解析.
,(2)详见解析.
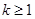 ,(2)详见解析.
,(2)详见解析.试题分析:(1)不等式恒成立问题,通常利用变量分离法转化为求最值问题. 由
 , 则
, 则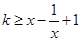 ,不等式
,不等式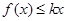 恒成立就转化为
恒成立就转化为 ,又
,又 在
在 上是增函数,
上是增函数, 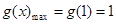 ,所以
,所以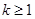 .(2)证明判断函数
.(2)证明判断函数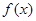 在
在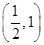 内存在零点,关键利用零点存在性定理.
内存在零点,关键利用零点存在性定理. ,
,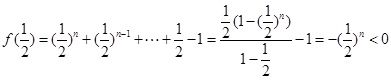 由零点存在性定理有
由零点存在性定理有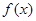 在
在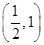 内至少存在一个的零点.
内至少存在一个的零点. 试题解析:[解] (1)由
 , 则
, 则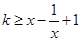 , 2分
, 2分又
 在
在 上是增函数,
上是增函数, 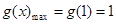 4分
4分所以
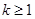 . 6分
. 6分(2)
 是增函数,且
是增函数,且 , 8分
, 8分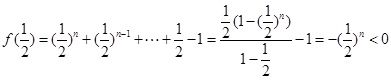 12分
12分所以
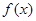 在
在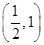 内存在唯一的零点. 14分
内存在唯一的零点. 14分
练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 ,且有
,且有 .
. ,且
,且 ;
; 在区间
在区间 内有两个不同的零点.
内有两个不同的零点. ,则
,则 =________.
=________. +
+ +…+
+…+ =________.
=________. ,
, ,
, ,映射
,映射 .对于直线
.对于直线 上任意一点
上任意一点 ,
, ,若
,若 ,我们就称
,我们就称 为直线
为直线
 ,则映射
,则映射


 ,若f(a)=4,则实数a=( )
,若f(a)=4,则实数a=( )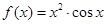 在区间
在区间 内的图象大致为( )
内的图象大致为( )
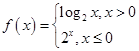 若
若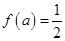 ,则
,则