题目内容
已知函数
(Ⅰ)求函数 的单调区间和最小值;
的单调区间和最小值;
(Ⅱ)若函数 在
在 上是最小值为
上是最小值为 ,求
,求 的值;
的值;
(Ⅲ)当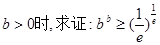 (其中
(其中 ="2.718" 28…是自然对数的底数).
="2.718" 28…是自然对数的底数).
(Ⅰ)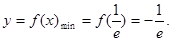 (Ⅱ)
(Ⅱ)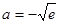 ;(Ⅲ)
;(Ⅲ)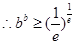 .
.
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
已知函数
(Ⅰ)求函数 的单调区间和最小值;
的单调区间和最小值;
(Ⅱ)若函数 在
在 上是最小值为
上是最小值为 ,求
,求 的值;
的值;
(Ⅲ)当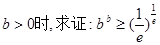 (其中
(其中 ="2.718" 28…是自然对数的底数).
="2.718" 28…是自然对数的底数).
(Ⅰ)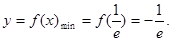 (Ⅱ)
(Ⅱ)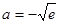 ;(Ⅲ)
;(Ⅲ)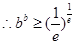 .
.
解析

 名校课堂系列答案
名校课堂系列答案