题目内容
【题目】已知椭圆![]() 的中心为坐标原点,其离心率为
的中心为坐标原点,其离心率为![]() ,椭圆
,椭圆![]() 的一个焦点和抛物线
的一个焦点和抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆![]() 的方程
的方程![]()
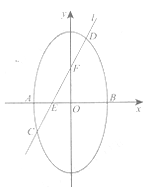
(2)过点![]() 的动直线
的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,试问:在平面上是否存在一个定点
两点,试问:在平面上是否存在一个定点![]() ,使得无论
,使得无论![]() 如何转动,以
如何转动,以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,若存在,说出点
,若存在,说出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
【答案】(1)![]() (2)定点
(2)定点![]()
【解析】
试题分析:(1)先设处椭圆的标准方程,根据离心率求的a和c的关系,进而根据抛物线的焦点求得c,进而求得a,则b可得,进而求的椭圆的标准方程;(2)若直线l与x轴重合,则以AB为直径的圆是![]() ,若直线l垂直于x轴,则以AB为直径的圆是
,若直线l垂直于x轴,则以AB为直径的圆是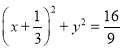 .联立两个圆的方程求得其交点的坐标,推断两圆相切,进而可判断因此所求的点T如果存在,只能是这个切点.证明时先看直线l垂直于x轴时,以AB为直径的圆过点T(1,0).再看直线l不垂直于x轴,可设出直线方程,与圆方程联立消去y,记点A
.联立两个圆的方程求得其交点的坐标,推断两圆相切,进而可判断因此所求的点T如果存在,只能是这个切点.证明时先看直线l垂直于x轴时,以AB为直径的圆过点T(1,0).再看直线l不垂直于x轴,可设出直线方程,与圆方程联立消去y,记点A ![]() ,B
,B ![]() ,根据韦达定理求得
,根据韦达定理求得![]() 和
和![]() 的表达式,代入
的表达式,代入![]() 的表达式中,求得
的表达式中,求得![]() ,进而推断TA⊥TB,即以AB为直径的圆恒过点T(1,0).
,进而推断TA⊥TB,即以AB为直径的圆恒过点T(1,0).
试题解析:(1)抛物线焦点的坐标为![]() ,则椭圆
,则椭圆![]() 的焦点在
的焦点在![]() 轴上
轴上![]()
设椭圆方程为![]()
由题意可得![]() ,
,![]() ,
,![]() ,
,
∴ 椭圆方程为![]() ……3分
……3分
(2)若直线![]() 与
与![]() 轴重合,则以
轴重合,则以![]() 为直径的圆是
为直径的圆是![]() ,
,
若直线![]() 垂直于
垂直于![]() 轴,则以
轴,则以![]() 为直径的圆是
为直径的圆是
由 即两圆相切于点
即两圆相切于点![]() ……5分因此所求的点
……5分因此所求的点![]() 如果存在,只能是
如果存在,只能是![]() ,事实上,点
,事实上,点![]() 就是所求的点. ……6分
就是所求的点. ……6分
证明:当直线![]() 垂直于
垂直于![]() 轴时,以
轴时,以![]() 为直径的圆过点
为直径的圆过点![]() ,若直线
,若直线![]() 不垂直于
不垂直于![]() 轴,
轴,
可设直线![]() :
:![]() 设点
设点![]() ,
,![]()
由
![]() , ∴
, ∴  ……9分
……9分
又 ![]()
![]() ,
,![]() ,
,
∴ ![]()
![]()
![]()

![]() ……11分
……11分
∴ ![]() 即:
即:![]()
![]() 故以
故以![]() 为直径的圆恒过点
为直径的圆恒过点![]() .
.
综上可知:在坐标平面上存在一个定点![]() 满足条件. ……12分
满足条件. ……12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目