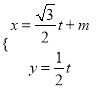题目内容
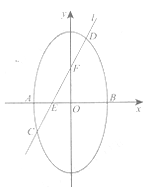
【题目】椭圆![]() 短轴的左右两个端点分别为A,B,直线
短轴的左右两个端点分别为A,B,直线![]() 与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.
与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线AD,CB的斜率分别为![]() ,若
,若![]() ,求k的值.
,求k的值.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)联立直线方程与椭圆方程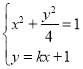 ,消去未知数
,消去未知数![]() 得到关于
得到关于![]() 的方程为:
的方程为:![]() ,
,![]() 显然成立,设
显然成立,设![]() ,于是可以得出
,于是可以得出![]() 和
和![]() ,根据直线
,根据直线![]() 求得
求得![]() ,
,![]() ,于是根据
,于是根据![]() 有:
有:![]() ,就可以求出
,就可以求出![]() 的值;(2)
的值;(2)![]() ,所以
,所以![]() ,则平方有
,则平方有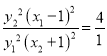 (*),又因为
(*),又因为![]() ,
,![]() ,代入(*)得:
,代入(*)得: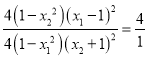 ,于是整理可得:
,于是整理可得:![]() ,整理后得到关于
,整理后得到关于![]() 和
和![]() 的表达式,即得到关于
的表达式,即得到关于![]() 的表达式,于是可以求出
的表达式,于是可以求出![]() 值.
值.
试题解析:(I)设![]()
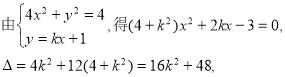
![]()
由已知![]()
又![]()
所以![]()
所以![]() ,
,
符合题意,
所以,所求直线l的方程为![]()
(II)![]() ,
,![]() ,
,
所以![]()
平方得![]()
![]() 代入上式,
代入上式,
计算得![]()
所以![]()
因为![]()
所以k=3

练习册系列答案
相关题目
【题目】为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
145.5~149.5 | 1 | 0.02 |
149.5~153.5 | 4 | 0.08 |
153.5~157.5 | 20 | 0.40 |
157.5~161.5 | 15 | 0.30 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 | m | n |
合 计 | M | N |
(1)求出表中![]() 所表示的数分别是多少?
所表示的数分别是多少?
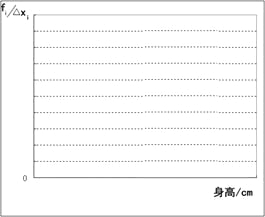
(2)画出频率分布直方图.
(3)全体女生中身高在哪组范围内的人数最多?由直方图确定此组数据中位数是多少?