��Ŀ����
����Ŀ����a��b�������x�IJ���ʽa2x��b2(1��x)��[ax��b(1��x)]2��
���𰸡�{x|0��x��1}��
��������
��ԭ����ʽ����Ϊ(a��b)2(x2��x) ��0���������õ�ϵ��(a��b)2��0��ֱ�ӽ������ʽx2��x��0����.
�⣺��ԭ����ʽ��Ϊ
(a2��b2)x+b2��(a��b)2x2��2(a��b)bx��b2��
���������� (a��b)2(x2��x) ��0����
�� a��b �� (a��b)2��0��
�� x2��x��0��
�� x(x��1) ��0��
��˲���ʽ���ý⼯ {x|0��x��1}��
���㾦��
��С����Ҫ���鲻��ʽ����֪ʶ������ʽ�Ľⷨ������ʱҪע�ʽ��������ã����ں��εĶ��β���ʽ���⣬���ж϶�����ϵ���ǷΣ��������۲�������0��������0���ٿ�ʽ���ܷ���ʽ�ֽ⣬���ܹ���ʽ�ֽ�����зֽ⣬�ٱȽ�������С,���ͼ��õ�����ʽ�Ľ⼯.
�����͡������
��������
19
����Ŀ����Sn�ǵȲ�����{an}��ǰn��ͣ���֪![]() ��
��![]() �ĵȱ�����Ϊ
�ĵȱ�����Ϊ![]() ����
����![]() ��
��![]() �ĵȲ�����Ϊ1��������{an}��ͨ�ʽ��
�ĵȲ�����Ϊ1��������{an}��ͨ�ʽ��
���𰸡�![]() ��
��![]() .
.
��������
��Ȳ�����{an}������Ϊa1������Ϊd�����õȲ�����͵ȱ�����Ķ��壬���õȲ����е����ʽ���������a1��d���ⷽ�̿���ͨ��an��
��Ȳ�����{an}������![]() ,����Ϊ
,����Ϊ![]() ����ͨ��Ϊ
����ͨ��Ϊ![]() ��
��
ǰ![]() ���Ϊ
���Ϊ![]() ����������
����������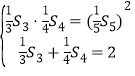 ,
,
����![]() ���ɴ˿ɵ�
���ɴ˿ɵ�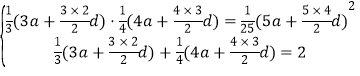 ,
,
������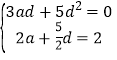 , �ⷽ�����
, �ⷽ�����![]() ��
��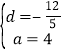 ,
,
�ɴ˵�![]() ����
����![]() .
.
������![]() ��
��![]() ��������.
��������.
��������Ȳ����е�ͨ�ʽΪ![]() ��
��![]() .
.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�