题目内容
【题目】已知函数 
。
（1）求函数
的定义域和值域；
（2）设
（
为实数），求
在
时的最大值
；
（3）对（2）中，若
对所有的实数及
恒成立，求实数
的取值范围。
【答案】（1）定义域为
，值域为
（2）
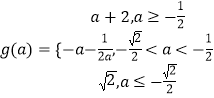（3）
【解析】试题分析：（1）由偶次根式被开方数非负列不等式解得定义域，先平方得
，即得函数值域 （2）转化为一元二次函数在定义区间上最值问题，按对称轴与定义区间位置关系讨论，最大值取法，（3）先求
最小值，将不等式恒成立转化为二次不等式
在定义区间上恒成立，结合图像可知
，解不等式可得实数
的取值范围
试题解析：解：由1+x≥0且1-x≥0，得-1≤x≤1,所以定义域为
又由
得值域为
（2）因为
因为a<0时,①若
， 
②若
，即
则
③若
， 
综上有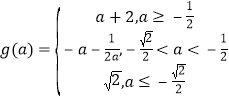
（3）易得
，所以
解得
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
