题目内容
2．已知a为常数，函数f（x）=x（lnx-ax）有两个极值点x1，x2（x1＜x2），则（ ）| A． | f（x1）＜0，f（x2）＜-$\frac{1}{2}$ | B． | f（x1）＞0，f（x2）＞-$\frac{1}{2}$ | C． | f（x1）＜0，f（x2）＞-$\frac{1}{2}$ | D． | f（x1）＞0，f（x2）＜-$\frac{1}{2}$ |
分析 先求出f′（x），令f′（x）=0，由题意可得lnx=2ax-1有两个解x1，x2?函数g（x）=lnx+1-2ax有且只有两个零点?g′（x）在（0，+∞）上的唯一的极值不等于0．利用导数与函数极值的关系即可得出．
解答 解：∵f（x）=x（lnx-ax），
∴f′（x）=lnx+1-2ax，（x＞0）
令f′（x）=0，由题意可得lnx=2ax-1有两个解x1，x2?函数g（x）=lnx+1-2ax有且只有两个零点?g′（x）在（0，+∞）上的唯一的极值不等于0．
g′（x）=$\frac{1-2ax}{x}$．
①当a≤0时，g′（x）＞0，f′（x）单调递增，因此g（x）=f′（x）至多有一个零点，不符合题意，应舍去．
②当a＞0时，令g′（x）=0，解得x=$\frac{1}{2a}$，
∵x∈（0，$\frac{1}{2a}$），g′（x）＞0，函数g（x）单调递增；x∈（$\frac{1}{2a}$，+∞）时，g′（x）＜0，函数g（x）单调递减．
∴x=$\frac{1}{2a}$是函数g（x）的极大值点，则g（$\frac{1}{2a}$）＞0，
即ln$\frac{1}{2a}$+1-1=-ln（2a）＞0，
∴ln（2a）＜0，∴0＜2a＜1，即0＜a＜$\frac{1}{2}$．
∵$0＜{x}_{1}＜\frac{1}{2a}＜{x}_{2}$，f′（x1）=lnx1+1-2ax1=0，f′（x2）=lnx2+1-2ax2=0．
且f（x1）=x1（lnx1-ax1）=x1（2ax1-1-ax1）=x1（ax1-1）＜x1（-ax1）=$-a{{x}_{1}}^{2}$＜0，
f（x2）＞f（$\frac{1}{2a}$），f（$\frac{1}{2a}$）=$\frac{1}{2a}$（ln$\frac{1}{2a}$-$\frac{1}{2}$），
令h（x）=x（lnx-$\frac{1}{2}$），（x＞1）．
h′（x）=lnx+1-$\frac{1}{2}$=lnx+$\frac{1}{2}$＞0，函数h（x）＞h（1）=-$\frac{1}{2}$，
∴$f（{x}_{2}）＞-\frac{1}{2}$．
故选：C．
点评 本题考查了利用导数研究函数极值的方法，考查了分类讨论的思想方法，考查了推理能力与计算能力，属于难题．
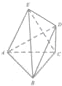已知AC=BC=$\sqrt{2}$，CD=$\frac{\sqrt{3}}{2}$，AB=BE=EA=2，CD⊥面ABC，面ABE⊥面ABC．
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）一个顶点为A（0，1），直线l：y=-x+2恰好与椭圆相切．