题目内容
【题目】已知函数![]()
(1)若![]() 存在极值点1,求
存在极值点1,求![]() 的值;
的值;
(2)若![]() 存在两个不同的零点
存在两个不同的零点![]() ,求证:
,求证:![]()
【答案】(1) ![]() ;(2) 见解析.
;(2) 见解析.
【解析】
试题(1)由![]() 存在极值点为1,得
存在极值点为1,得![]() ,可解得a.
,可解得a.
(2)是典型的极值点偏移问题,先证明![]() ,再利用
,再利用![]() 在
在![]() 上的单调性,即可得证.
上的单调性,即可得证.
试题解析:(1) ![]() ,因为
,因为![]() 存在极值点为1,所以
存在极值点为1,所以![]() ,即
,即![]() ,经检验符合题意,所以
,经检验符合题意,所以![]() .
.
(2) ![]()
①当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上为增函数,不符合题意;
上为增函数,不符合题意;
②当![]() 时,由
时,由![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,所
,所![]() 为减函数,
为减函数,
所以当![]() 时,
时,![]() 取得极小值
取得极小值![]()
又因为![]() 存在两个不同零点
存在两个不同零点![]() ,所以
,所以![]() ,即
,即![]()
整理得![]() ,
,
作![]() 关于直线
关于直线![]() 的对称曲线
的对称曲线![]() ,
,
令![]()
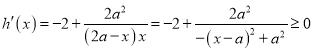
所以![]() 在
在![]() 上单调递增,
上单调递增,
不妨设![]() ,则
,则![]() ,
,
即![]() ,
,
又因为![]() 且
且![]() 在
在![]() 上为减函数,
上为减函数,
故![]() ,即
,即![]() ,又
,又![]() ,易知
,易知![]() 成立,
成立,
故![]() .
.
点晴:本题主要考查导数在函数中的应用,具体涉及到函数的极值,函数的极值点偏移问题.第一问中![]() 存在极值点1,所以
存在极值点1,所以![]() ,解得
,解得![]() ;第二问处理极值点问题有两个关键步骤:一是在
;第二问处理极值点问题有两个关键步骤:一是在![]() 构造函数
构造函数![]() 证明其大于于0恒成立,二是利用
证明其大于于0恒成立,二是利用![]() 在
在![]() 上为减函数 ,两者结合即可证明结论成立.
上为减函数 ,两者结合即可证明结论成立.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
【题目】已知国家某![]() 级大型景区对拥挤等级与每日游客数量
级大型景区对拥挤等级与每日游客数量![]() (单位:百人)的关系有如下规定:当
(单位:百人)的关系有如下规定:当![]() 时,拥挤等级为“优”;当
时,拥挤等级为“优”;当![]() 时,拥挤等级为“良”;当
时,拥挤等级为“良”;当![]() 时,拥挤等级为“拥挤”;当
时,拥挤等级为“拥挤”;当![]() 时,拥挤等级为“严重拥挤”.该景区对6月份的游客数量作出如图的统计数据:
时,拥挤等级为“严重拥挤”.该景区对6月份的游客数量作出如图的统计数据:
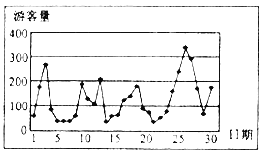
(1)下面是根据统计数据得到的频率分布表,求出![]() 的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
游客数量(单位:百人) |
|
|
|
|
天数 |
| 10 | 4 | 1 |
频率 |
|
|
|
|
(2)某人选择在6月1日至6月5日这5天中任选2天到该景区游玩,求他这2天遇到的游客拥挤等级均为“优”的频率.