题目内容
【题目】已知圆![]() 与圆
与圆![]() .
.
(1)求证两圆相交;
(2)求两圆公共弦所在直线的方程;
(3)求过两圆的交点且圆心在直线![]() 上的圆的方程.
上的圆的方程.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)将圆的方程化为标准方程,求出圆心距及半径,即可证明两圆相交;
(2)对两圆的方程作差即可得出两圆的公共弦所在的直线方程;
(3)先求两圆的交点,进而可求圆的圆心与半径,从而可求圆的方程.
试题解析:
(1)证明:圆![]() 与圆
与圆![]() 化为标准方程分别为圆
化为标准方程分别为圆![]() 与圆
与圆![]() ,
,
![]() 与圆
与圆![]() ,半径都为
,半径都为![]()
![]() 圆心距为
圆心距为![]() ,两圆相交.
,两圆相交.
(2)解:将两圆的方程作差即可得出两圆的公共弦所在的直线方程,即
![]() ,
,
即![]() .
.
(3)解:由(2)得![]() 代入圆
代入圆![]() ,化简可得
,化简可得![]() ,
,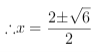 ,当
,当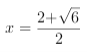 时,
时,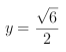 ;当
;当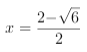 时,
时,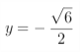 设所求圆的圆心坐标为
设所求圆的圆心坐标为![]() ,则
,则
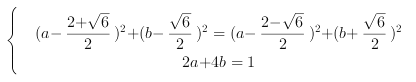 ,
,
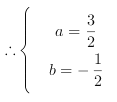 ,
,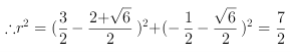 ,
,
![]() 过两圆的交点且圆心在直线
过两圆的交点且圆心在直线![]() 上的圆的方程为
上的圆的方程为![]() .
.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如下表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?


