题目内容
【题目】设![]() 为
为![]() 的内心,三边长
的内心,三边长![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,若直线
,若直线![]() 交直线
交直线![]() 于点
于点![]() ,则线段
,则线段![]() 的长为______.
的长为______.
【答案】![]()
【解析】
设内切圆⊙I与三角形三边分别相切于点O,D,E.IO⊥AB,建立直角坐标系.分别设AO=x,BO=y,CD=z.利用切线的性质定理可得x,y,z.利用余弦定理可得cosB=![]() ,sinB,tanB,可得直线BC的方程.设内切圆的半径为r.则
,sinB,tanB,可得直线BC的方程.设内切圆的半径为r.则![]() =
=![]() ,解得r,得I坐标,可得直线PI的方程,联立直线BC和PI解得Q.即可得|CQ|=6﹣|BQ|.
,解得r,得I坐标,可得直线PI的方程,联立直线BC和PI解得Q.即可得|CQ|=6﹣|BQ|.
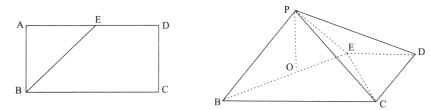
如图所示,设内切圆⊙I与三角形三边分别相切于点O,D,E,IO⊥AB,建立直角坐标系.
分别设AO=x,BO=y,CD=z,则 ,解得x=3,y=4,z=2.O(0,0),B(4,0),P(﹣1,0),
,解得x=3,y=4,z=2.O(0,0),B(4,0),P(﹣1,0),
在![]() 中,cosB=
中,cosB=![]() =
=![]() ,sinB=
,sinB=![]() ,可得tanB=
,可得tanB=![]() .
.
直线BC的方程为:y=![]() (x﹣4).
(x﹣4).
设内切圆的半径为r.则![]() =
=![]() ,解得r=
,解得r=![]() .可得I
.可得I .
.
直线PI的方程为:y= x+
x+![]() ,即y=
,即y=![]() x+
x+![]() .
.
联立 ,解得Q
,解得Q ,
,
∴|CQ|=6﹣|BQ|=6﹣ =6﹣
=6﹣![]() =
=![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案【题目】某地因受天气,春季禁渔等因素影响,政府规定每年的7月1日以后的100天为当年的捕鱼期.某渔业捕捞队对吨位为![]() 的20艘捕鱼船一天的捕鱼量进行了统计,如下表所示:
的20艘捕鱼船一天的捕鱼量进行了统计,如下表所示:
捕鱼量(单位:吨) |
|
|
|
|
|
频数 | 2 | 7 | 7 | 3 | 1 |
根据气象局统计近20年此地每年100天的捕鱼期内的晴好天气情况如下表(捕鱼期内的每个晴好天气渔船方可捕鱼,非晴好天气不捕鱼):
晴好天气(单位:天) |
|
|
|
|
|
频数 | 2 | 7 | 6 | 3 | 2 |
(同组数据以这组数据的中间值作代表)
(Ⅰ)估计渔业捕捞队吨位为![]() 的渔船一天的捕鱼量的平均数;
的渔船一天的捕鱼量的平均数;
(Ⅱ)若以(Ⅰ)中确定的平均数作为上述吨位的捕鱼船在晴好天气捕鱼时一天的捕鱼量.
①估计一艘上述吨位的捕鱼船一年在捕鱼期内的捕鱼总量;
②已知当地鱼价为2万元/吨,此种捕鱼船在捕鱼期内捕鱼时,每天成本为10万元/艘;若不捕鱼,每天成本为2万元/艘,请依据往年天气统计数据,估计一艘此种捕鱼船年利润不少于1600万元的概率.