题目内容
【题目】求满足下列条件的双曲线的标准方程:
(1)一条渐近线方程为![]() ,且与椭圆
,且与椭圆![]() 有相同的焦点;
有相同的焦点;
(2)经过点![]() ,且与双曲线
,且与双曲线![]() 有共同的渐近线.
有共同的渐近线.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意设出双曲线的标准方程![]() ,根据渐近线方程和
,根据渐近线方程和![]() 间的关系求出
间的关系求出![]() 后可得所求方程;或根据渐近线方程设双曲线方程为
后可得所求方程;或根据渐近线方程设双曲线方程为![]() ,然后由题意求出
,然后由题意求出![]() 后得到所求.(2)根据题意设双曲线的方程为
后得到所求.(2)根据题意设双曲线的方程为![]() ,代入点
,代入点![]() 的坐标求出
的坐标求出![]() 后可得所求方程.
后可得所求方程.
(1)方法1:椭圆方程可化为![]() ,焦点坐标为
,焦点坐标为![]() ,
,
故可设双曲线的方程为![]() ,其渐近线方程为
,其渐近线方程为![]() ,
,
则![]() ,
,
又![]() ,
,
所以可得![]() ,
,![]() ,
,
所以所求双曲线的标准方程为![]() .
.
方法2:由于双曲线的一条渐近线方程为![]() ,则另一条渐近线方程为
,则另一条渐近线方程为![]() .
.
故可设双曲线的方程为![]() ,即
,即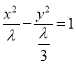 ,
,
因为双曲线与椭圆![]() 共焦点,
共焦点,
所以![]() ,
,
即![]() ,
,
解得![]() ,
,
所以所求双曲线的标准方程为![]() .
.
(2)由题意可设所求双曲线方程为![]() ,
,
因为点![]() 在双曲线上,
在双曲线上,
∴![]() ,解得
,解得![]() ,
,
所以所求双曲线的标准方程为![]() .
.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目