题目内容
3.已知曲线f(x)=-x3-2x2+2ax+8在(1,f(1))处切线与直线x-3y+1=0垂直.(Ⅰ)求f(x)解析式;
(Ⅱ)求f(x)的单调区间、极值并画出y=f(x)的大致图象.
分析 (Ⅰ)求出函数的导数,求得切线的斜率,由直线垂直的条件:斜率之积为-1,即可得到a=2,进而得到f(x)的解析式;
(Ⅱ)求出函数的导数,令导数大于0,可得增区间,令导数小于0,可得减区间,进而得到极值和函数的图象.
解答 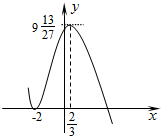 解:(Ⅰ)对f(x)求导f′(x)=-3x2-4x+2a,
解:(Ⅰ)对f(x)求导f′(x)=-3x2-4x+2a,
由题意f′(1)=-3-4+2a=-3,∴a=2,
∴f(x)=-x3-2x2+4x+8.
(Ⅱ)f′(x)=-3x2-4x+4=-(3x-2)(x+2),
由f′(x)≥0得$-2≤x≤\frac{2}{3}$,由f′(x)≤0得$x≥\frac{2}{3}$或x≤-2,
∴单调增区间为$[{-2,\frac{2}{3}}]$,单减区间为(-∞,-2),$(\frac{2}{3},+∞)$,
f(x)极小值=f(-2)=0f(x)极大值=$f(\frac{2}{3})=9\frac{13}{27}$,
大致图象如右图.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值,主要考查导数的几何意义,函数的单调性的判断,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
14.已知圆C1:(x+2)2+(y-3)2=5与圆C2相交于A(0,2),B(-1,1)两点,且四边形C1AC2B为平行四形,则圆C2的方程为( )
| A. | (x-1)2+y2=5 | B. | (x-1)2+y2=$\frac{9}{2}$ | C. | (x-$\frac{1}{2}$)2+(y-$\frac{1}{2}$)2=5 | D. | (x-$\frac{1}{2}$)2+(y-$\frac{1}{2}$)2=$\frac{9}{2}$ |
18.若f(x)=$\frac{lnx}{x}$,e<b<a,则( )
| A. | f(a)>f(b) | B. | f(a)=f(b) | C. | f(a)<f(b) | D. | f(a)f(b)>1 |
8.已知sin(3π+α)=$\frac{1}{3}$,则cos2α等于( )
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{8}{9}$ | D. | -$\frac{8}{9}$ |
13.$C_7^4+C_7^5+C_8^6$等于( )
| A. | $C_9^5$ | B. | $C_9^6$ | C. | $C_8^7$ | D. | $C_9^7$ |
 正方体ABCD-A1B1C1D1中,E,F分别是BC,C1D1的中点.
正方体ABCD-A1B1C1D1中,E,F分别是BC,C1D1的中点.