题目内容
(2013·天津高考)已知抛物线y2=8x的准线过双曲线
-
=1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为____________.
x2-
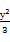=1
解析
练习册系列答案
小学教材完全解读系列答案
相关题目
小学教材完全解读系列答案题目内容
(2013·天津高考)已知抛物线y2=8x的准线过双曲线-=1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为____________.
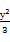x2-=1
解析
小学教材完全解读系列答案
过点
．
的方程，并求其准线方程；
且斜率为
的直线
与抛物线交于
两点，求
的面积．
的焦点为
，则
________，
向其准线作垂线，记与抛物线的交点为
，则
_____.
是椭圆
上的点，则
的取值范围是 ．
到双曲线
的一条渐近线的距离为
，则双曲线
的离心率为 ．
的焦点为
，其准线经过双曲线
，
的左顶点，点
为这两条曲线的一个交点，且
，则双曲线的渐近线的方程为_______．
（
）的焦距为
，右顶点为
，抛物线
的焦点为
,若双曲线截抛物线的准线所得线段长为
，则双曲线的渐近线方程为___________.
- 
=1相交于A，B两点，若△ABF为等边三角形，则p=___________.
－y2＝1的顶点到其渐近线的距离等于________．