题目内容
7.已知集合P={x|x≤m+3},Q={x|m2-1<x<2m+2},若P?Q,则实数m的取值范围为m≤1或m≥3.分析 结合题意,由P?Q,分类讨论,可得不等式,由此解得实数m的取值范围.
解答 解:∵集合P={x|x≤m+3},Q={x|m2-1<x<2m+2},P?Q,
∴有Q=∅,即m2-1≥2m+2,∴m≤-1或m≥3;
Q≠∅,即m2-1<2m+2,∴-1<m<3
∵P?Q,∴2m+2≤m+3解得m≤1,
∴-1<m≤1,
综上,m≤1或m≥3.
故答案为:m≤1或m≥3.
点评 本题主要考查集合关系中参数的取值范围问题,集合间的关系,正确分类讨论是解题的关键,属于中档题.

练习册系列答案
相关题目
2.已知两点M(-3,0),N(3,0),点P为坐标平面内的动点,且|$\overrightarrow{MN}$|•|$\overrightarrow{MP}$|=$\overrightarrow{MN}$•$\overrightarrow{PN}$,若Q为直线2x+y-9=0上一点,则|$\overrightarrow{PQ}$|的最小值为( )
| A. | $\frac{15}{2}$ | B. | $\frac{\sqrt{15}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{3\sqrt{5}}{2}$ |
8.在200m高的山顶上,测得山下一塔顶与塔底的俯角分别是30°,60°,如图所示则塔高CB为( ) 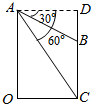

| A. | $\frac{400}{3}$ m | B. | $\frac{400}{3}$$\sqrt{3}$ m | C. | $\frac{200}{3}$$\sqrt{3}$ m | D. | $\frac{200}{3}$ m |
5.在△ABC中,若(a+b+c)(c+b-a)-bc=0,则∠A=( )
| A. | 120° | B. | 150° | C. | 60° | D. | 30° |