题目内容
1.有关下列命题的说法正确的是( )| A. | 命题“若x2=1,则x=1”的否命题为:若“x2=1则x≠1” | |
| B. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若sinx≠siny,则x≠y”为真命题 |
分析 写出命题的否命题判断A;求解方程x2-5x-6=0判断B;写出特称命题的否定判断C;由sinx≠siny得x≠y判断D.
解答 解:命题“若x2=1,则x=1”的否命题为:若“x2≠1则x≠1”,A错误;
由x=-1,得x2-5x-6=0,由x2-5x-6=0,得x=-1或x=6.
∴“x=-1”是“x2-5x-6=0”的充分不必要条件,B错误;
命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1≥0”,C错误;
命题“若sinx≠siny,则x≠y”为真命题,D正确.
故选:D.
点评 本题考查命题的真假判断与应用,考查了否命题、命题的否定,训练了充分必要条件的判定方法,是中档题.

练习册系列答案
相关题目
12.在复平面内,O为原点,向量$\overrightarrow{OA}$对应的复数为-1-2i,若点A关于直线y=-x的对称点为B,则向量$\overrightarrow{OB}$对应的复数为( )
| A. | -2-i | B. | 1+2i | C. | 2+i | D. | -1+2i |
16.己知f(x)=x2-2x+2,在[$\frac{1}{4}$,m2-m+2]上任取三个数a,b,c,均存在以 f(a),f(b),f(c)为三边的三角形,则m的取值范围为( )
| A. | (0,1) | B. | [0,$\frac{\sqrt{2}}{2}$) | C. | (0,$\frac{\sqrt{2}}{2}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] |
11.如图所示,程序框图(算法流程图)输出的结果是( )
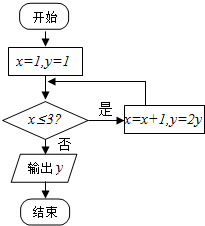

| A. | 2 | B. | 4 | C. | 8 | D. | 16 |