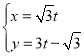题目内容
【题目】2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式，此事引起了国际数学界的轰动许多专家认为这是数论研究中的一项重大突破世界主流媒体都对这项重要成果作了报道并给予了高度评价，印度媒体甚至称赞张益唐为“中国的拉马努金”.孪生素数猜想是希尔伯特在1900年提出的23个问题之一，可以这样描述：存在无穷多个素数
，使得
是素数，素数对
称为孪生素数.在不超过20的素数中，随机选取两个不同的数，其中能够组成孪生素数的概率是（ ）
A.
B.
C.
D.
【答案】D
【解析】
根据已知条件可求出不超过20的素数有8个，从中随机选取两个共有28种不同的情况，而不超过20的素数组成的孪生素数对有4个，根据古典概型计算公式即可得到答案．
不超过20的素数有2，3，5，7，11，13，17，19共计8个，
从中随机选取两个共有28种不同的情况，
根据素数对
为孪生素数，
所以不超过20的素数组成的孪生素数对为
共有4个，
故能够组成的字孪生素数的概率
.
故选:D.
三点一测快乐周计划系列答案【题目】千百年来，我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化，总结了丰富的“看云识天气”的经验，并将这些经验编成谚语，如“天上钩钩云，地上雨淋淋”“日落云里走，雨在半夜后”……小波同学为了验证“日落云里走，雨在半夜后”，观察了所在地区A的100天日落和夜晚天气，得到如下
列联表：
夜晚天气 日落云里走 | 下雨 | 未下雨 |
出现 | 25 | 5 |
未出现 | 25 | 45 |
临界值表 | ||||
P（ | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
并计算得到
，下列小波对地区A天气判断不正确的是（ ）
A.夜晚下雨的概率约为
B.未出现“日落云里走”夜晚下雨的概率约为
C.有
的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
D.出现“日落云里走”，有的把握认为夜晚会下雨
【题目】2019新型冠状病毒（2019―nCoV）于2020年1月12日被世界卫生组织命名.冠状病毒是一个大型病毒家族，可引起感冒以及中东呼吸综合征（MERS）和严重急性呼吸综合征（SARS）等较严重疾病.某医院对病患及家属是否带口罩进行了调查，统计人数得到如下列联表：
戴口罩 | 未戴口罩 | 总计 | |
未感染 | 30 | 10 | 40 |
感染 | 4 | 6 | 10 |
总计 | 34 | 16 | 50 |
（1）根据上表，判断是否有95%的把握认为未感染与戴口罩有关；
（2）从上述感染者中随机抽取3人，记未戴口罩的人数为
，求的分布列和数学期望.
参考公式：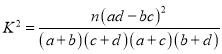
，其中
.
参考数据：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某单位为了更好地应对新型冠状病毒肺炎疫情，对单位的职工进行防疫知识培训，所有职工选择网络在线培训和线下培训中的一种方案进行培训.随机抽取了140人的培训成绩，统计发现样本中40个成绩来自线下培训职工，其余来自在线培训的职工，并得到如下统计图表：
线下培训茎叶图在线培训直方图
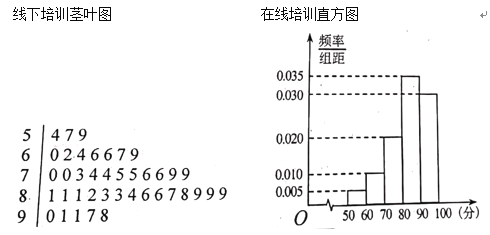
（1）得分90分及以上为成绩优秀，完成下边列联表，并判断是否有
的把握认为成绩优秀与培训方式有关？
优秀 | 非优秀 | 合计 | |
线下培训 | |||
在线培训 | |||
合计 |
（2）成绩低于60分为不合格.在样本的不合格个体中随机再抽取3个，其中在线培训个数是
，求分布列与数学期望.
附：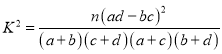
．
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
