题目内容
【题目】千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区A的100天日落和夜晚天气,得到如下![]() 列联表:
列联表:
夜晚天气 日落云里走 | 下雨 | 未下雨 |
出现 | 25 | 5 |
未出现 | 25 | 45 |
临界值表 | ||||
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
并计算得到![]() ,下列小波对地区A天气判断不正确的是( )
,下列小波对地区A天气判断不正确的是( )
A.夜晚下雨的概率约为![]()
B.未出现“日落云里走”夜晚下雨的概率约为![]()
C.有![]() 的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
D.出现“日落云里走”,有![]() 的把握认为夜晚会下雨
的把握认为夜晚会下雨
【答案】D
【解析】
把频率看作概率,即可判断![]() 的正误;根据独立性检验可判断
的正误;根据独立性检验可判断![]() 的正误,即得答案.
的正误,即得答案.
由题意,把频率看作概率可得:
夜晚下雨的概率约为![]() ,故
,故![]() 正确;
正确;
未出现“日落云里走”夜晚下雨的概率约为![]() ,故
,故![]() 正确;
正确;
由![]() ,根据临界值表,可得有
,根据临界值表,可得有![]() 的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关,故
的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关,故![]() 正确;
正确;
故![]() 错误.
错误.
故选:![]() .
.

【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
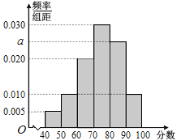
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |