题目内容
【题目】如图所示,已知三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .
.
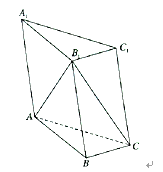
(1)求证: ![]() ;
;
(2)若![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析: (1)证明线面垂直,一般利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的寻找与论证往往需要结合平几知识,如利用等腰三角形性质得底边上中线垂直底面得线线垂直,(2)一般利用空间向量数量积求二面角大小,先根据条件确定恰当空间直角坐标系,设立各点坐标,利用方程组求各面法向量,利用向量数量积求法向量夹角余弦值,最后根据法向量夹角与二面角关系确定二面角的余弦值.
试题解析:(1)∵四边形![]() 为平行四边形,且
为平行四边形,且![]() ,
, ![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
取![]() 中点
中点![]() ,连接
,连接![]() ,
, ![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)∵![]() 为等边三角形,
为等边三角形, ![]() ,∴
,∴![]() ,
,
∵在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∵![]() ,
, ![]() ,∴
,∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() .
.
以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 方向为
方向为![]() ,
, ![]() ,
, ![]() 轴的正向,建立如图所示的坐标系,
轴的正向,建立如图所示的坐标系, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
则平面![]() 的一个法向量
的一个法向量![]() ,
,
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则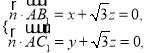 令
令![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴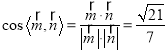 .
.

点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.

【题目】心理学家分析发现“喜欢空间想象”与“性别”有关,某数学兴趣小组为了验证此结论,从全体组员中按分层抽样的方法抽取50名同学(男生30人、女生20人),给每位同学立体几何题、代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如下表:(单位:人)
立体几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(2)经统计得,选择做立体几何题的学生正答率为![]() ,且答对的学生中男生人数是女生人数的5倍,现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行研究,记抽取的两人中答对的人数为
,且答对的学生中男生人数是女生人数的5倍,现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行研究,记抽取的两人中答对的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
【题目】已知随机变量![]() 的取值为不大于
的取值为不大于![]() 的非负整数值,它的分布列为:
的非负整数值,它的分布列为:
| 0 | 1 | 2 |
| n |
|
|
|
|
|
|
其中![]() (
(![]() )满足:
)满足: ![]() ,且
,且![]() .
.
定义由![]() 生成的函数
生成的函数![]() ,令
,令![]() .
.
(I)若由![]() 生成的函数
生成的函数![]() ,求
,求![]() 的值;
的值;
(II)求证:随机变量![]() 的数学期望
的数学期望![]() ,
, ![]() 的方差
的方差![]() ;
;
(![]() )
)
(Ⅲ)现投掷一枚骰子两次,随机变量![]() 表示两次掷出的点数之和,此时由
表示两次掷出的点数之和,此时由![]() 生成的函数记为
生成的函数记为![]() ,求
,求![]() 的值.
的值.
【题目】为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在30名男性驾驶员中,平均车速超过![]() 的有20人,不超过
的有20人,不超过![]() 的有10人.在20名女性驾驶员中,平均车速超过
的有10人.在20名女性驾驶员中,平均车速超过![]() 的有5人,不超过
的有5人,不超过![]() 的有15人.
的有15人.
(Ⅰ)完成下面的列联表,并判断是否有![]() 的把握认为平均车速超过
的把握认为平均车速超过![]() 的人与性别有关;
的人与性别有关;
平均车数超过
| 平均车速不超过
| 合计 | |
男性驾驶员人数 | |||
女性驾驶员人数 | |||
合计 |
(Ⅱ)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随即抽取3辆,记这3辆车中驾驶员为女性且车速不超过![]() 的车辆数为
的车辆数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列和数学期望
的分布列和数学期望
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】(本小题满分12分) 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过![]() ):
):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
|
|
|
|
该社团将该校区在![]() 年
年![]() 天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
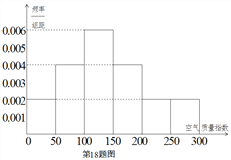
(Ⅰ)请估算![]() 年(以
年(以![]() 天计算)全年空气质量优良的天数(未满一天按一天计算);
天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)该校![]() 年
年![]() 月
月![]() 、
、![]() 日将作为高考考场,若这两天中某天出现
日将作为高考考场,若这两天中某天出现![]() 级重度污染,需要净化空气费用
级重度污染,需要净化空气费用![]() 元,出现
元,出现![]() 级严重污染,需要净化空气费用
级严重污染,需要净化空气费用![]() 元,记这两天净化空气总费用为
元,记这两天净化空气总费用为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.