题目内容
【题目】定义:对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() ,试判断
,试判断![]() 是否为定义域
是否为定义域![]() 上的“局部奇函数”?若是,求出所有满足
上的“局部奇函数”?若是,求出所有满足![]() 的
的![]() 的值;若不是,请说明事由.
的值;若不是,请说明事由.
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围.
的取值范围.
(3)若![]() 为定义域
为定义域![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 为“局部奇函数”;(2)
为“局部奇函数”;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(Ⅰ)由已知中“局部奇函数”的定义,结合函数![]() ,可得结论;
,可得结论;
(Ⅱ)若![]() 是定义在
是定义在![]() 上的“局部奇函数”,则
上的“局部奇函数”,则![]() 有解,即可求解实数
有解,即可求解实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() 是定义域上的“局部奇函数”,则
是定义域上的“局部奇函数”,则![]() 有解,使用换元法和根据二次函数的性质,即可得到实数
有解,使用换元法和根据二次函数的性质,即可得到实数![]() 的取值范围;
的取值范围;
试题解析:
(1)当![]() ,方程
,方程![]() 即
即![]() ,
,
![]() ,所以
,所以![]() 为“局部奇函数”.
为“局部奇函数”.
(2)法一:当![]() 时,
时,![]() 可化为
可化为![]() ,
,
∵![]() 有定义域为
有定义域为![]() ,所以方程
,所以方程![]() 在
在![]() 有解,
有解,
令![]() ,则
,则![]() ,
,
∵![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
∴当![]() 时,
时,![]() ,即
,即![]() ,
,
∴![]() .
.
法二:当![]() 时,
时,![]() 可化为
可化为![]() ,
,
令![]() ,则关于
,则关于![]() 的二次方程
的二次方程![]() 在
在![]() 上有解即可,
上有解即可,
保证![]() 为“局部奇函数”,设
为“局部奇函数”,设![]() .
.
①当方程![]() 在
在![]() 上只有一解时,
上只有一解时,
须满足在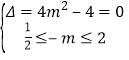 或
或![]() ,
,
解得![]() 或
或![]() 舍去,
舍去,
因为此时方程在区间![]() 有两解,不符合这种情况.
有两解,不符合这种情况.
②当方程![]() 在
在![]() 上有两个不相等实根时,
上有两个不相等实根时,
须满足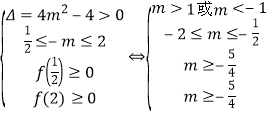 ,
,
解得![]() ,∴
,∴![]() .
.
(3)当![]() 为定义域
为定义域![]() 上的“局部奇函数”时,
上的“局部奇函数”时,![]() ,
,
可化为![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
从而![]() 在
在![]() 有解,即可保证
有解,即可保证![]() 为“局部奇函数”
为“局部奇函数”
令![]() ,则
,则
①![]() 时,
时,![]() 在
在![]() 有解,
有解,
即![]() ,解得
,解得![]() .
.
②当![]() ,
,![]() 在
在![]() 有解等价于,
有解等价于,
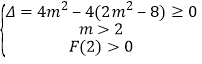 ,解得
,解得![]() .
.
综上,![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】为了对某课题进行讨论研究,用分层抽样的方法从三所高校A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
高校 | 相关人数 | 抽取人数 |
A | x | 1 |
B | 36 | y |
C | 54 | 3 |
(1)求x、y;
(2)若从高校B相关的人中选2人作专题发言,应采用什么抽样法,请写出合理的抽样过程.