题目内容
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() ,在以O为极点,x轴的非负半轴为极轴的极坐标系中,直线l的极坐标方程为
,在以O为极点,x轴的非负半轴为极轴的极坐标系中,直线l的极坐标方程为![]() .
.
(1)设曲线C与直线l的交点为A、B,求弦AB的中点P的直角坐标;
(2)动点Q在曲线C上,在(1)的条件下,试求△OPQ面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先把曲线![]() 和直线
和直线![]() 化成普通方程,再联立根据韦达定理和中点公式可得
化成普通方程,再联立根据韦达定理和中点公式可得![]() 的坐标;
的坐标;
(2)先求出OP的长度和直线OP的方程,根据曲线![]() 的参数方程设出
的参数方程设出![]() 的坐标,求出
的坐标,求出![]() 到直线OP的距离得最大值,再求出面积.
到直线OP的距离得最大值,再求出面积.
由![]() 消去参数
消去参数![]() ,得
,得![]() ,
,
由![]() 得
得![]() ,得
,得![]() ,
,
联立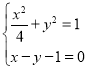 消去
消去![]() 并整理得
并整理得![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,![]() .
.
(2)|OP|=![]() =
=![]() ,
,
所以直线OP的方程为x+4y=0,
设Q(2cosα,sinα),
则点Q到直线x+4y=0的距离d=![]() ≤
≤![]() =
=![]() ,
,
![]() =
=![]() |OP|d≤
|OP|d≤![]() ×
×![]() ×
×![]() =
=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】已知鲜切花![]() 的质量等级按照花枝长度
的质量等级按照花枝长度![]() 进行划分,划分标准如下表所示.
进行划分,划分标准如下表所示.
花枝长度 |
|
|
|
鲜花等级 | 三级 | 二级 | 一级 |
某鲜切花加工企业分别从甲乙两个种植基地购进鲜切花![]() ,现从两个种植基地购进的鲜切花
,现从两个种植基地购进的鲜切花![]() 中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
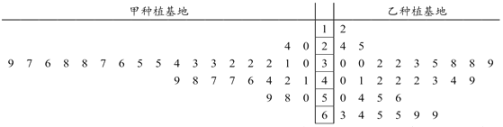
(1)根据茎叶图比较两个种植基地鲜切花![]() 的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
(2)若从等级为三级的样品中随机选取2个进行新产品试加工,求选取的2个全部来自乙种植基地的概率;
(3)根据该加工企业的加工和销售记录,了解到来自乙种植基地的鲜切花![]() 的加工产品的单件利润为4元;来自乙种植基地的鲜切花
的加工产品的单件利润为4元;来自乙种植基地的鲜切花![]() 的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
三级花加工产品 | 二级花加工产品 | 一级花加工产品 | |
销售率 |
|
|
|
单价/(元/件) | 12 | 16 | 20 |
由于鲜切花![]() 加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花
加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花![]() ?
?