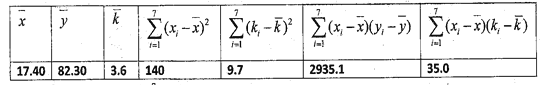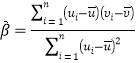题目内容
【题目】已知点![]() 是抛物线
是抛物线![]() 的对称轴与准线的交点,点
的对称轴与准线的交点,点![]() 为抛物线的焦点,
为抛物线的焦点, ![]() 在抛物线上且满足
在抛物线上且满足![]() ,当
,当![]() 取最大值时,点
取最大值时,点![]() 恰好在以
恰好在以![]() ,
, ![]() 为焦点的双曲线上,则双曲线的离心率为( )
为焦点的双曲线上,则双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】过P作准线的垂线,垂足为N,
则由抛物线的定义可得|PN|=|PB|,
∵|PA|=m|PB|,
∴|PA|=m|PN|
∴![]() =
=![]() ,
,
设PA的倾斜角为α,则sinα=![]() ,
,
当m取得最大值时,sinα最小,此时直线PA与抛物线相切,
设直线PA的方程为y=kx﹣1,代入x2=4y,可得x2=4(kx﹣1),
即x2﹣4kx+4=0,
∴△=16k2﹣16=0,∴k=±1,
∴P(2,1),
∴双曲线的实轴长为PA﹣PB=2(![]() ﹣1),
﹣1),
∴双曲线的离心率为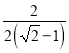 =
=![]() .
.
故选:A.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】某市县乡教师流失现象非常严重,为了县乡孩子们能接受良好教育,某市今年要为两所县乡中学招聘储备未来三年的教师,现在每招聘一名教师需要1万元,若三年后教师严重短缺时再招聘,由于各种因素,则每招聘一名教师需要3万元,已知现在该市县乡中学无多余教师,为决策应招聘多少县乡教师搜集并整理了该市50所县乡中学在过去三年内的教师流失数,得到如表的频率分布表:
流失教师数 | 6 | 7 | 8 | 9 |
频数 | 10 | 15 | 15 | 10 |
以这50所县乡中学流失教师数的频率代替一所县乡中学流失教师数发生的概率,记![]() 表示两所县乡中学在过去三年共流失的教师数,
表示两所县乡中学在过去三年共流失的教师数, ![]() 表示今年为两所县乡中学招聘的教师数.为保障县乡孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘.
表示今年为两所县乡中学招聘的教师数.为保障县乡孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘.
(1)求![]() 的分布列;
的分布列;
(2)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(3)以未来四年内招聘教师所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
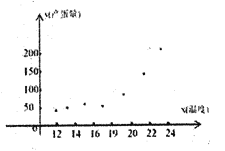
【题目】某地![]() 户家庭的年收入
户家庭的年收入![]() (万元)和年饮食支出
(万元)和年饮食支出![]() (万元)的统计资料如下表:
(万元)的统计资料如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;(结果保留到小数点后
的线性回归方程;(结果保留到小数点后![]() 为数字)
为数字)
(2)利用(1)中的回归方程,分析这![]() 户家庭的年饮食支出的变化情况,并预测该地年收入
户家庭的年饮食支出的变化情况,并预测该地年收入![]() 万元的家庭的年饮食支出.(结果保留到小数点后
万元的家庭的年饮食支出.(结果保留到小数点后![]() 位数字)
位数字)
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
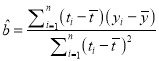 ,
, ![]()