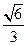题目内容
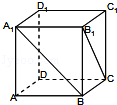
如图,在三棱柱 中,侧棱
中,侧棱 底面
底面 ,
, 为
为 的中点,
的中点, ,
, .
.

(1)求证: 平面
平面 ;
;
(2)求四棱锥 的体积.
的体积.
 中,侧棱
中,侧棱 底面
底面 ,
, 为
为 的中点,
的中点, ,
, .
.
(1)求证:
 平面
平面 ;
;(2)求四棱锥
 的体积.
的体积.(1)见解析;(2)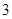 .
.
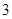 .
.试题分析:(1)欲证
 平面
平面 ,根据线面平行的判定定理可知只需证
,根据线面平行的判定定理可知只需证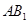 与平面
与平面 内一直线平行,连接
内一直线平行,连接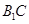 ,设
,设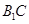 与
与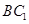 相交于点O,连接
相交于点O,连接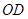 ,根据中位线定理可知
,根据中位线定理可知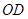 ∥
∥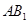 ,
,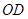 ?平面
?平面 ,
,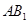 ?平面
?平面 ,满足定理所需条件;
,满足定理所需条件;(2)根据面面垂直的判定定理可知平面
 ⊥平面
⊥平面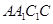 ,作
,作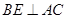 ,垂足为E,则
,垂足为E,则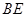 ⊥平面
⊥平面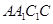 ,然后求出棱长,最后根据四棱锥
,然后求出棱长,最后根据四棱锥 ,的体积
,的体积 ,即可求四棱锥
,即可求四棱锥 的体积.
的体积.
(1)证明:连接
 ,设
,设 与
与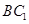 相交于点
相交于点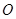 ,连接
,连接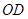 ,
,∵ 四边形
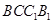 是平行四边形,
是平行四边形, ∴点
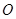 为
为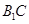 的中点.
的中点. ∵
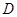 为
为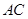 的中点,
的中点,∴
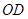 为△
为△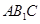 的中位线,
的中位线,∴
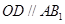 .
. ∵
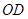
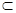 平面
平面 ,
,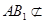 平面
平面 ,
,∴
 平面
平面 .
. (2)∵
 平面
平面 ,
,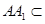 平面
平面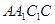 ,
,∴ 平面

 平面
平面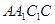 ,且平面
,且平面
 平面
平面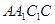
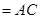 .
.作
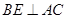 ,垂足为
,垂足为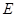 ,则
,则 平面
平面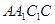 ,
,∵
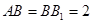 ,
,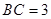 ,
,在Rt△
 中,
中,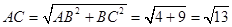 ,
,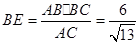 ,
,∴四棱锥
 的体积
的体积
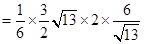
 .
.∴四棱锥
 的体积为
的体积为 .
.
练习册系列答案
相关题目

 ,
, ,
, ,N是BC的中点.如图所示,将梯形ABCD绕AB逆时针旋转
,N是BC的中点.如图所示,将梯形ABCD绕AB逆时针旋转 ,得到梯形
,得到梯形 .
.
 平面
平面 ;
;  平面
平面 ;
;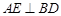 于
于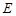 (不同于点
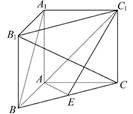
(不同于点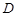 ),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥
),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥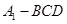 ,如图2所示.
,如图2所示.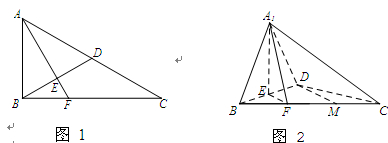
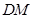 //平面
//平面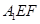 ;
;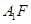 ;
;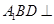 平面
平面 ,试判断直线
,试判断直线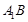 与直线CD能否垂直?并说明理由.
与直线CD能否垂直?并说明理由.