题目内容
(2011•湖北)如图,已知正三棱柱ABC=A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.
(1)当CF=1时,求证:EF⊥A1C;
(2)设二面角C﹣AF﹣E的大小为θ,求tanθ的最小值.

(1)当CF=1时,求证:EF⊥A1C;
(2)设二面角C﹣AF﹣E的大小为θ,求tanθ的最小值.

(1)见解析 (2)

(1)过E作EN⊥AC于N,连接EF,NF,AC1,由直棱柱的性质可知,底面ABC⊥侧面A1C
∴EN⊥侧面A1C
NF为EF在侧面A1C内的射影
在直角三角形CNF中,CN=1
则由 ,得NF∥AC1,又AC1⊥A1C,故NF⊥A1C
,得NF∥AC1,又AC1⊥A1C,故NF⊥A1C
由三垂线定理可知EF⊥A1C
(2)连接AF,过N作NM⊥AF与M,连接ME
由(1)可知EN⊥侧面A1C,根据三垂线定理得EM⊥AF
∴∠EMN是二面角C﹣AF﹣E的平面角即∠EMN=θ
设∠FAC=α则0°<α≤45°,
在直角三角形CNE中,NE= ,在直角三角形AMN中,MN=3sinα
,在直角三角形AMN中,MN=3sinα
故tanθ= ,又0°<α≤45°∴0<sinα≤
,又0°<α≤45°∴0<sinα≤
故当α=45°时,tanθ达到最小值,
tanθ= ,此时F与C1重合
,此时F与C1重合
∴EN⊥侧面A1C
NF为EF在侧面A1C内的射影
在直角三角形CNF中,CN=1
则由
 ,得NF∥AC1,又AC1⊥A1C,故NF⊥A1C
,得NF∥AC1,又AC1⊥A1C,故NF⊥A1C由三垂线定理可知EF⊥A1C
(2)连接AF,过N作NM⊥AF与M,连接ME
由(1)可知EN⊥侧面A1C,根据三垂线定理得EM⊥AF
∴∠EMN是二面角C﹣AF﹣E的平面角即∠EMN=θ
设∠FAC=α则0°<α≤45°,
在直角三角形CNE中,NE=
 ,在直角三角形AMN中,MN=3sinα
,在直角三角形AMN中,MN=3sinα故tanθ=
 ,又0°<α≤45°∴0<sinα≤
,又0°<α≤45°∴0<sinα≤
故当α=45°时,tanθ达到最小值,
tanθ=
 ,此时F与C1重合
,此时F与C1重合
练习册系列答案
相关题目
 的侧棱与底面垂直,且
的侧棱与底面垂直,且 ,
, ,
, ,
, ,点
,点 、
、 、
、 分别为
分别为 、
、 、
、 的中点.
的中点.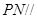 平面
平面 ;
; 面
面 ;
; 的距离.
的距离.
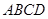 是边长为2的正方形,
是边长为2的正方形,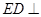 平面
平面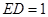 ,
,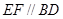 ,且
,且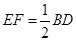 .
.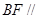 平面
平面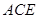 ;
;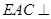 平面
平面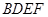 ;
; 的体积。
的体积。
 中,侧棱
中,侧棱 底面
底面 ,
, 为
为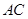 的中点,
的中点, ,
, .
.
 平面
平面 ;
; 的体积.
的体积.
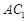 各棱所在直线中,与棱
各棱所在直线中,与棱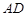 所在直线互为异面直线的有 条.
所在直线互为异面直线的有 条.
 为60°,A、B是棱
为60°,A、B是棱 上的两点,AC、BD分别在半平面
上的两点,AC、BD分别在半平面 内,
内, ,
, ,且AB=AC=
,且AB=AC= ,BD=
,BD= ,则CD的长为( )
,则CD的长为( ) C.
C.