题目内容
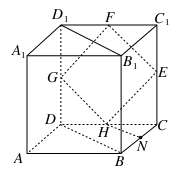
(2014·海淀模拟)如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.
(1)求证:A1B∥平面AEC1.
(2)求证:B1C⊥平面AEC1.

(1)求证:A1B∥平面AEC1.
(2)求证:B1C⊥平面AEC1.
(1)见解析 (2)见解析
(1)连接A1C交AC1于点O,连接EO,
因为ACC1A1为正方形,所以O为A1C中点.
又E为CB中点,所以EO为△A1BC的中位线,
所以EO∥A1B.
又EO?平面AEC1,A1B?平面AEC1,
所以A1B∥平面AEC1.
(2)因为AB=AC,又E为CB中点,
所以AE⊥BC,
又因为在直三棱柱ABC-A1B1C1中,
BB1⊥底面ABC,
又AE?底面ABC,所以AE⊥BB1,
又因为BB1∩BC=B,所以AE⊥平面BCC1B1,
又B1C?平面BCC1B1,
所以AE⊥B1C.
在矩形BCC1B1中,
tan∠BCB1=tan∠EC1C=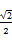 ,
,
所以∠BCB1=∠EC1C,
所以∠BCB1+∠CEC1=90°,
即B1C⊥EC1.
又AE∩EC1=E,所以B1C⊥平面AEC1.
因为ACC1A1为正方形,所以O为A1C中点.
又E为CB中点,所以EO为△A1BC的中位线,
所以EO∥A1B.
又EO?平面AEC1,A1B?平面AEC1,
所以A1B∥平面AEC1.
(2)因为AB=AC,又E为CB中点,
所以AE⊥BC,
又因为在直三棱柱ABC-A1B1C1中,
BB1⊥底面ABC,
又AE?底面ABC,所以AE⊥BB1,
又因为BB1∩BC=B,所以AE⊥平面BCC1B1,
又B1C?平面BCC1B1,
所以AE⊥B1C.
在矩形BCC1B1中,
tan∠BCB1=tan∠EC1C=
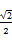 ,
,所以∠BCB1=∠EC1C,
所以∠BCB1+∠CEC1=90°,
即B1C⊥EC1.
又AE∩EC1=E,所以B1C⊥平面AEC1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是边长为2的正方形,
是边长为2的正方形, 平面
平面 ,
,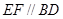 ,且
,且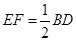 .
.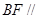 平面
平面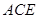 ;
;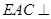 平面
平面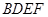 ;
;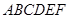 的体积。
的体积。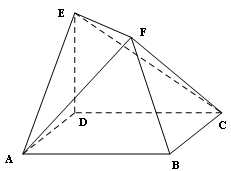
 中,侧棱
中,侧棱 底面
底面 ,
, 为
为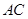 的中点,
的中点, ,
, .
.
 平面
平面 ;
; 的体积.
的体积.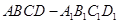 中,
中,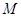 是
是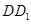 的中点.
的中点. 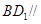 平面
平面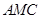 ;
;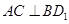 ;
;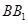 上是否存在点
上是否存在点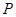 ,当
,当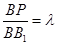 时,平面
时,平面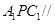 平面
平面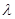 的值并证明;若不存在,请说明理由.
的值并证明;若不存在,请说明理由.
 都为正方形,
都为正方形, ,F
,F 的中点,E为线段BC上的动点.
的中点,E为线段BC上的动点.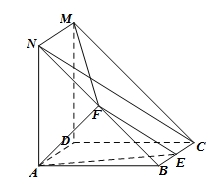
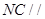 平面AEF;
平面AEF;
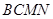 平面;
平面;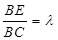 ,写出
,写出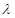 为何值时MF⊥平面AEF(结论不要求证明).
为何值时MF⊥平面AEF(结论不要求证明).