题目内容
【题目】定义在R上的函数f（x）满足：f（2）=1，且对于任意的x∈R，都有f′（x）＜ 
，则不等式f（log2x）＞ 
的解集为 ．
【答案】{x丨0＜x＜4}
【解析】解：设F（x）=f（x）﹣ 
x，求导F′（x）=f′（x）﹣ ＜0，则F（x）在R单调递减， 由f（log2x）＞ 
，即f（log2x）﹣ log2x＞ ，
由f（2）﹣ ×2= ，
∴F（log2x）＞F（2），（x＞0），
则log2x＜2，解得：0＜x＜4，
∴不等式的解集为：{x丨0＜x＜4}，
故答案为：：{x丨0＜x＜4}．
故答案为：{x丨0＜x＜4}．
构造辅助函数，求导，由题意可知F（x）=f（x）﹣ x在R单调递减，原不等式转化成F（log2x）＞F（2），（x＞0），根据函数的单调性即可求得不等式的解集．
练习册系列答案
相关题目
【题目】对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
分组 | 频数 | 频率 |
[10，15） | 10 | 0.25 |
[15，20） | 25 | n |
[20，25） | m | p |
[25，30） | 2 | 0.05 |
合计 | M | 1 |
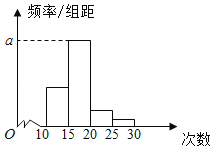
（1）求出表中M，p及图中a的值；
（2）若该校高一学生有360人，试估计该校高一学生参加社区服务的次数在区间[15，20）内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，请列举出所有基本事件，并求至多1人参加社区服务次数在区间[20，25）内的概率．