题目内容
(1)如图所示,证明命题“a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥b,则a⊥c”为真.


(2)写出上述命题的逆命题,并判断其真假(不需证明).


(2)写出上述命题的逆命题,并判断其真假(不需证明).
(1)见解析(2)逆命题为:a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥c,则a⊥b.真命题
(1)记c∩b=A,P为直线b上异于点A的任意一点,过P作PO⊥π,垂足为O,则O∈c.
因为PO⊥π,a?π,
所以直线PO⊥a.
又a⊥b,b?平面PAO,PO∩b=P,
所以a⊥平面PAO.
又c?平面PAO,
所以a⊥c.
(2)逆命题为:a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥c,则a⊥b.逆命题为真命题.
因为PO⊥π,a?π,
所以直线PO⊥a.
又a⊥b,b?平面PAO,PO∩b=P,
所以a⊥平面PAO.
又c?平面PAO,
所以a⊥c.
(2)逆命题为:a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥c,则a⊥b.逆命题为真命题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ),连接MN.
),连接MN.

 的值.
的值.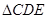 中
中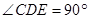 ,平面
,平面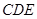 外一条线段AB满足AB∥DE,AB
外一条线段AB满足AB∥DE,AB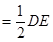 ,AB⊥AC,F是CD的中点.
,AB⊥AC,F是CD的中点.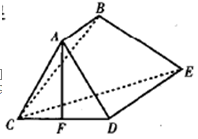
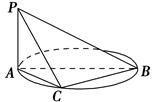
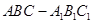 中,点
中,点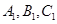 在平面ABC内的正投影分别为A,B,C,且
在平面ABC内的正投影分别为A,B,C,且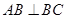 ,
,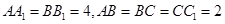 ,E为
,E为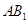 中点,
中点,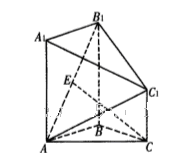
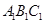 ,
,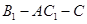 的大小.
的大小.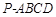 中,四边形
中,四边形 是菱形,
是菱形,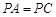 ,E为PB的中点.
,E为PB的中点.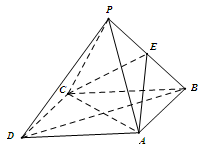
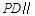 平面
平面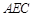 ;
;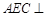 平面
平面 .
. 
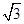 时,求PB的长.
时,求PB的长.