题目内容
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=2,∠BAD=60°.
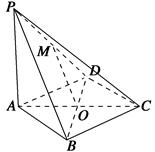
(1)求证:OM∥平面PAB;
(2)求证:平面PBD⊥平面PAC;
(3)当四棱锥P-ABCD的体积等于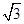 时,求PB的长.
时,求PB的长.

(1)求证:OM∥平面PAB;
(2)求证:平面PBD⊥平面PAC;
(3)当四棱锥P-ABCD的体积等于
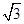 时,求PB的长.
时,求PB的长.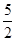
(1)证明∵在△PBD中,O,M分别是BD,PD的中点,∴OM是△PBD的中位线,∴OM∥PB.
∵OM?平面PAB,PB?平面PAB,∴OM∥平面PAB.
(2)证明∵底面ABCD是菱形,∴BD⊥AC.∵PA⊥平面ABCD,BD?平面ABCD,∴PA⊥BD.又AC?平面PAC,PA?平面PAC,AC∩PA=A,∴BD⊥平面PAC.∵BD?平面PBD,∴平面PBD⊥平面PAC.
(3)解∵底面ABCD是菱形,AB=2,∠BAD=60°,
∴S菱形ABCD=2×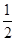 ×AB×AD×sin 60°=2×2×
×AB×AD×sin 60°=2×2×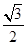 =2
=2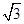 .
.
∵四棱锥P-ABCD的高为PA,∴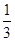 ×2
×2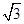 ×PA=
×PA=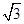 ,解得PA=
,解得PA=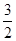 .又∵PA⊥平面ABCD,AB?平面ABCD,∴PA⊥AB.在Rt△PAB中,PB=
.又∵PA⊥平面ABCD,AB?平面ABCD,∴PA⊥AB.在Rt△PAB中,PB= 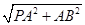 =
=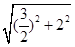 =
=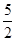 .
.
∵OM?平面PAB,PB?平面PAB,∴OM∥平面PAB.
(2)证明∵底面ABCD是菱形,∴BD⊥AC.∵PA⊥平面ABCD,BD?平面ABCD,∴PA⊥BD.又AC?平面PAC,PA?平面PAC,AC∩PA=A,∴BD⊥平面PAC.∵BD?平面PBD,∴平面PBD⊥平面PAC.
(3)解∵底面ABCD是菱形,AB=2,∠BAD=60°,
∴S菱形ABCD=2×
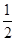 ×AB×AD×sin 60°=2×2×
×AB×AD×sin 60°=2×2×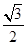 =2
=2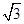 .
.∵四棱锥P-ABCD的高为PA,∴
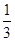 ×2
×2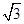 ×PA=
×PA=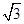 ,解得PA=
,解得PA=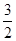 .又∵PA⊥平面ABCD,AB?平面ABCD,∴PA⊥AB.在Rt△PAB中,PB=
.又∵PA⊥平面ABCD,AB?平面ABCD,∴PA⊥AB.在Rt△PAB中,PB= 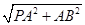 =
=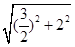 =
=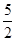 .
.
练习册系列答案
相关题目


 的底面
的底面 是矩形,平面
是矩形,平面 ⊥平面
⊥平面 分别为
分别为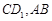 的中点.
的中点.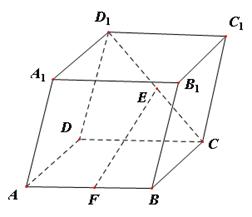
 ;(2)
;(2) ∥平面
∥平面 .
. ,点F是PB的中点,点E在边BC上移动
,点F是PB的中点,点E在边BC上移动
 ,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ= .
,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ= .
 ,
, 是两条不同的直线,
是两条不同的直线, ,
, ,
, 是三个不同的平面.有下列四个命题:
是三个不同的平面.有下列四个命题: ,
, ,
, ,则
,则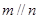 ;
; ,
, ,则
,则 ;
; ,
, ,
, ;
; ,
, ,
,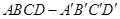 的棱长为1,
的棱长为1,  分别是棱
分别是棱 ,
, 的中点,过直线
的中点,过直线 的平面分别与棱
的平面分别与棱 、
、 交于
交于 ,设
,设 ,
, ,给出以下四个命题:
,给出以下四个命题:

 平面
平面 ;
; 时,四边形
时,四边形 ,
, 的体积
的体积 为常函数;
为常函数;