题目内容
如图,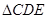 中
中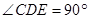 ,平面
,平面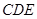 外一条线段AB满足AB∥DE,AB
外一条线段AB满足AB∥DE,AB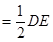 ,AB⊥AC,F是CD的中点.
,AB⊥AC,F是CD的中点.
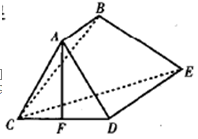
(1)求证:AF∥平面BCE
(2)若AC=AD,证明:AF⊥平面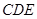
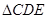 中
中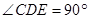 ,平面
,平面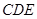 外一条线段AB满足AB∥DE,AB
外一条线段AB满足AB∥DE,AB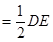 ,AB⊥AC,F是CD的中点.
,AB⊥AC,F是CD的中点.
(1)求证:AF∥平面BCE
(2)若AC=AD,证明:AF⊥平面
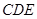
(1)详见解析;(2)详见解析
试题分析:(1)取
 的中点
的中点 ,连结
,连结 ,由中位线证得
,由中位线证得 ∥
∥ ,且
,且 ,再证
,再证 为平行四边形得
为平行四边形得 ∥
∥ ,即可得证
,即可得证 ∥平面
∥平面 。(2)先证
。(2)先证 ⊥平面
⊥平面 得
得 ,再根据等腰三角形中线即为高线证得
,再根据等腰三角形中线即为高线证得 ,即可证得
,即可证得 ⊥平面
⊥平面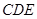 。
。试题解析:证明:
(1)如图,取
 的中点
的中点 ,连结
,连结

∵
 为
为 的中点
的中点∴
 ∥
∥ ,且
,且 2分
2分又∵

∴
 ∥
∥ 且
且
∴四边形
 为平行四边形
为平行四边形  ∥
∥  4分
4分又

 平面
平面 ,
,
 平面
平面
∴
 ∥平面
∥平面 6分
6分(2)∵
 ,
, 是
是 的中点
的中点∴
 7分
7分由
 ,
, ∥
∥ ,可得
,可得 ,
, 8分
8分且

 平面
平面 ,
,
 平面
平面 ,
,
∴
 ⊥平面
⊥平面 9分
9分∴
 10分
10分∵
 且
且 ,
,
∴
 ⊥平面
⊥平面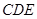 12分
12分
练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目



 中,点
中,点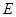 为边
为边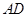 上的点,点
上的点,点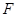 为边
为边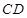 的中点,
的中点,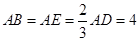 ,现将
,现将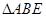 沿
沿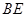 边折至
边折至 位置,且平面
位置,且平面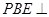 平面
平面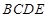 .
.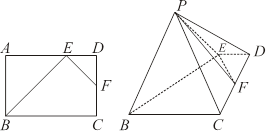
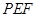 ;
;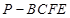 的体积.
的体积.
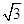 ,Q到a的距离为2
,Q到a的距离为2