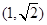题目内容
已知椭圆 的焦点为
的焦点为 ,
, ,在长轴
,在长轴 上任取一点
上任取一点 ,过
,过 作垂直于
作垂直于 的直线交椭圆于点
的直线交椭圆于点 ,则使得
,则使得 的点
的点 的概率为( )
的概率为( )
A. | B.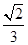 | C. | D. |
D
解析试题分析:∵ ,b=1,
,b=1,
设P( ),∴当
),∴当
 ,
,
解得y0= ,代入椭圆方程得x0=±
,代入椭圆方程得x0=± .由
.由 ,得∠F1PF2>90°.
,得∠F1PF2>90°.
∴结合题设条件可知使得 的M点的概率=
的M点的概率= .故选D.
.故选D.
考点:本题主要考查椭圆的几何性质,几何概型概率的计算。
点评:中档题,本题综合考查椭圆的几何性质,几何概型概率的计算。注意本题中 ,说明∠F1PF2>90°。
,说明∠F1PF2>90°。

练习册系列答案
相关题目
若双曲线 与直线
与直线 无交点,则离心率
无交点,则离心率 的取值范围( )
的取值范围( )
A. | B. | C. | D. |
过双曲线 的左焦点
的左焦点 作圆
作圆 的切线交双曲线右支于点
的切线交双曲线右支于点 ,切点为
,切点为 ,若
,若 ,则双曲线的离心率为
,则双曲线的离心率为
A. | B. | C. | D. |
 ,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点。设
,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点。设 ,则
,则 等于( )
等于( ) B.
B.  C.
C. D.
D. 
 是双曲线
是双曲线 上一点,
上一点, 、
、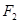 是其左、右焦点,
是其左、右焦点, 的三边长成等差数列,且
的三边长成等差数列,且 ,则双曲线的离心率等于
,则双曲线的离心率等于



 ,曲线C2:
,曲线C2: ,EF是曲线C1的任意一条直径,P是曲线C2上任一点,则
,EF是曲线C1的任意一条直径,P是曲线C2上任一点,则 ·
· 的最小值为 ( )
的最小值为 ( )
 的离心率为
的离心率为 .双曲线
.双曲线 的渐近线与椭圆
的渐近线与椭圆 有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆
有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆
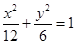


 与双曲线
与双曲线 相交于ABCD四点,若四边形ABCD是正方形,则双曲线的离心率的取值范围为( )
相交于ABCD四点,若四边形ABCD是正方形,则双曲线的离心率的取值范围为( )