题目内容
已知ABCD是矩形,PD=DC=a,AD=(1)求证:平面MNC⊥平面PBC;
(2)求点A到平面MNC的距离.
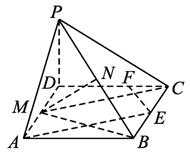
(方法一)证明:(1)连结PM,BM,PM=![]() =
=![]() ,
,
BM=![]() =
=![]() ,∴PM=BM,∴MN⊥PB,
,∴PM=BM,∴MN⊥PB,
又有:PC=![]() =
=![]() a,
a,

∴BC=PC,∴CN⊥PB,∴PB⊥平面MNC,∴平面MNC⊥平面PBC;
(2)取BC中点,NC中点,
易证得:AE∥MC,
故点A到平面MNC的距离就是点E到平面MNC的距离.
因PB⊥平面MNC,∴EF∥PB,
故EF⊥平面MNC,故点E到平面MNC的距离就是EF.
因EF=![]() ,因PB=
,因PB=![]() =2a,
=2a,
故EF=![]() .
.
故点A到平面MNC的距离是![]() .
.
(方法二)
(1)如图,建立空间直角坐标系D—XYZ,则:
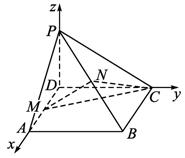
P(0,0,a),B(![]() a,a,0),M(
a,a,0),M(![]() ,0,0),C(0,a,0),N(
,0,0),C(0,a,0),N(![]() ,
,![]() ,
,![]() ).
).
![]() =(0,
=(0,![]() ,
,![]() ),
), ![]() =(
=(![]() ,-
,-![]() ,
,![]() ),
),![]() =(
=(![]() a,a,-a)
a,a,-a)
∴![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() .
.
∴PB⊥平面MNC,
∴平面PBC⊥平面MNC.
(2)由上可知:![]() ⊥
⊥![]() ,
,
设点A到平面MNC的距离为h,易知点N到平面ACM的距离为![]() ,
,
且:|![]() |=
|=![]() ,|
,|![]() |=a,故有:S△MNC=
|=a,故有:S△MNC=![]() |
|![]() |·|
|·|![]() |=
|=![]() ,又S△AMC=
,又S△AMC=![]() |
|![]() |·|
|·|![]() |=
|=![]() ,
,
因VA—MNC=VN—AMC,故有:h=![]() ,
,
即点A到平面MNC的距离是![]() .
.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 18、如图,已知ABCD是矩形,E是以CD为直径的半圆周上一点,且平面CDE⊥平面ABCD,求证:CE⊥平面ADE.
18、如图,已知ABCD是矩形,E是以CD为直径的半圆周上一点,且平面CDE⊥平面ABCD,求证:CE⊥平面ADE. 已知ABCD是矩形,AD=2AB,E,F分别是线段AB,BC的中点,PA⊥平面ABCD.
已知ABCD是矩形,AD=2AB,E,F分别是线段AB,BC的中点,PA⊥平面ABCD. 如图,已知ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点,PA=2,PD=AB,且平面MND⊥平面PCD.
如图,已知ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点,PA=2,PD=AB,且平面MND⊥平面PCD. 如图,已知ABCD是矩形,M、N分别是PC、PD上的点,MN⊥PC,且PA⊥平面ABCD,AN⊥PD,求证:AM⊥PC.
如图,已知ABCD是矩形,M、N分别是PC、PD上的点,MN⊥PC,且PA⊥平面ABCD,AN⊥PD,求证:AM⊥PC. (2013•内江二模)已知ABCD是矩形,AD=4,AB=2,E、F分别是AB、BC 的中点,PA丄面ABCD.
(2013•内江二模)已知ABCD是矩形,AD=4,AB=2,E、F分别是AB、BC 的中点,PA丄面ABCD.