题目内容
 已知ABCD是矩形,AD=2AB,E,F分别是线段AB,BC的中点,PA⊥平面ABCD.
已知ABCD是矩形,AD=2AB,E,F分别是线段AB,BC的中点,PA⊥平面ABCD.(Ⅰ)求证:DF⊥平面PAF;
(Ⅱ)在棱PA上找一点G,使EG∥平面PED,并说明理由.
分析:(Ⅰ)证明AF⊥FD,PA⊥FD,利用线面垂直的判定可得结论;
(Ⅱ)点G满足AG=
PA,利用线线平行可得线面平行,从而可得面面平行,进而可得线面平行.
(Ⅱ)点G满足AG=
| 1 |
| 4 |
解答: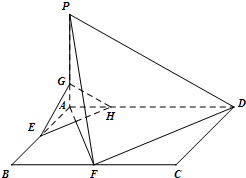 (Ⅰ)证明:在矩形ABCD中,
(Ⅰ)证明:在矩形ABCD中,
因为AD=2AB,点F是BC的中点,所以∠AFB=∠DFC=45°.
所以∠AFD=90°,即AF⊥FD. …(4分)
又PA⊥平面ABCD,所以PA⊥FD.
因为AF∩PA=A,所以FD⊥平面PAF. …(7分)
(Ⅱ)解:过E作EH∥FD交AD于H,则EH∥平面PFD,且AH=
AD.
再过H作HG∥PD交PA于G,所以GH∥平面PFD,且AG=
PA.
因为EH∩GH=H,所以平面EHG∥平面PFD. …(12分)
因为EG?平面EHG,所以EG∥平面PFD.
从而点G满足AG=
PA. …(14分)
 (Ⅰ)证明:在矩形ABCD中,
(Ⅰ)证明:在矩形ABCD中,因为AD=2AB,点F是BC的中点,所以∠AFB=∠DFC=45°.
所以∠AFD=90°,即AF⊥FD. …(4分)
又PA⊥平面ABCD,所以PA⊥FD.
因为AF∩PA=A,所以FD⊥平面PAF. …(7分)
(Ⅱ)解:过E作EH∥FD交AD于H,则EH∥平面PFD,且AH=
| 1 |
| 4 |
再过H作HG∥PD交PA于G,所以GH∥平面PFD,且AG=
| 1 |
| 4 |
因为EH∩GH=H,所以平面EHG∥平面PFD. …(12分)
因为EG?平面EHG,所以EG∥平面PFD.
从而点G满足AG=
| 1 |
| 4 |
点评:本题考查线面垂直的判定与性质,考查线面平行,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 18、如图,已知ABCD是矩形,E是以CD为直径的半圆周上一点,且平面CDE⊥平面ABCD,求证:CE⊥平面ADE.
18、如图,已知ABCD是矩形,E是以CD为直径的半圆周上一点,且平面CDE⊥平面ABCD,求证:CE⊥平面ADE. 如图,已知ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点,PA=2,PD=AB,且平面MND⊥平面PCD.
如图,已知ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点,PA=2,PD=AB,且平面MND⊥平面PCD. 如图,已知ABCD是矩形,M、N分别是PC、PD上的点,MN⊥PC,且PA⊥平面ABCD,AN⊥PD,求证:AM⊥PC.
如图,已知ABCD是矩形,M、N分别是PC、PD上的点,MN⊥PC,且PA⊥平面ABCD,AN⊥PD,求证:AM⊥PC. (2013•内江二模)已知ABCD是矩形,AD=4,AB=2,E、F分别是AB、BC 的中点,PA丄面ABCD.
(2013•内江二模)已知ABCD是矩形,AD=4,AB=2,E、F分别是AB、BC 的中点,PA丄面ABCD.