题目内容
 (2013•内江二模)已知ABCD是矩形,AD=4,AB=2,E、F分别是AB、BC 的中点,PA丄面ABCD.
(2013•内江二模)已知ABCD是矩形,AD=4,AB=2,E、F分别是AB、BC 的中点,PA丄面ABCD.(1)求证:PF丄DF;
(2)若PD与面ABCD所成角为300在PA上找一点 G,使EG∥面PFD,并求出AG的长.
分析:(1)证明:连接AF,要证PF⊥FD,只要证FD⊥平面PAF,只要证PA⊥FD,AF⊥FD即可.
(2)取AD中点I,取AI中点H,连接BI,EH,EG,GH,易知四边形BFDI是平行四边形,所以BI∥FD,再由E、H分别是AB、AI的中点,得到EH∥BI,由公理4可得EH∥FD,所以EH∥平面PFD,由
=
=
,所以GH∥PD,有HG∥平面PFD,转化为平面EHG∥平面PFD,得到EG∥平面PFD.
(2)取AD中点I,取AI中点H,连接BI,EH,EG,GH,易知四边形BFDI是平行四边形,所以BI∥FD,再由E、H分别是AB、AI的中点,得到EH∥BI,由公理4可得EH∥FD,所以EH∥平面PFD,由
| AG |
| AP |
| AH |
| AD |
| 1 |
| 4 |
解答: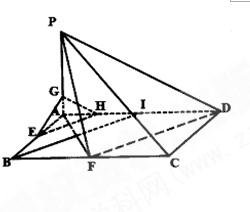 解:(1)证明:连接AF,
解:(1)证明:连接AF,
∵在矩形ABCD中,AD=4,AB=2,F是线段BC的中点,
∴FC=CD,∴△FCD是等腰直角三角形,
∴∠DFC=45°,同理可得∠AFB=45°,
∴AF⊥FD.
又∵PA⊥面ABCD,∴PA⊥FD,∵AF∩PA=A
∴FD⊥平面PAF,∴PF⊥FD.(6分)
(2)在AP上存在点G,
且AG=
AP,使得EG∥平面PFD,
证明:取AD中点I,取AI中点H,连接BI,EH,EG,GH,
∵DI∥BF,DI=BF,∴四边形BFDI是平行四边形,
∴BI∥FD
又∵E、H分别是AB、AI的中点,
∴EH∥BI,∴EH∥FD
而EH?平面PFD,∴EH∥平面PFD
∵
=
=
,
∴GH∥PD
而GH?平面PFD,
∴HG∥平面PFD,又∵EH∩GH=H
∴平面EHG∥平面PFD
∴EG∥平面PFD,从而G为所求.
由PD与面ABCD所成角为30°,∴∠PDA=30°,
在直角三角PAD中,∴AP=
=
,
∴AG=
AP=
.
 解:(1)证明:连接AF,
解:(1)证明:连接AF,∵在矩形ABCD中,AD=4,AB=2,F是线段BC的中点,
∴FC=CD,∴△FCD是等腰直角三角形,
∴∠DFC=45°,同理可得∠AFB=45°,
∴AF⊥FD.
又∵PA⊥面ABCD,∴PA⊥FD,∵AF∩PA=A
∴FD⊥平面PAF,∴PF⊥FD.(6分)
(2)在AP上存在点G,
且AG=
| 1 |
| 4 |
证明:取AD中点I,取AI中点H,连接BI,EH,EG,GH,
∵DI∥BF,DI=BF,∴四边形BFDI是平行四边形,
∴BI∥FD
又∵E、H分别是AB、AI的中点,
∴EH∥BI,∴EH∥FD
而EH?平面PFD,∴EH∥平面PFD
∵
| AG |
| AP |
| AH |
| AD |
| 1 |
| 4 |
∴GH∥PD
而GH?平面PFD,
∴HG∥平面PFD,又∵EH∩GH=H
∴平面EHG∥平面PFD
∴EG∥平面PFD,从而G为所求.
由PD与面ABCD所成角为30°,∴∠PDA=30°,
在直角三角PAD中,∴AP=
| AD | ||
|
4
| ||
| 3 |
∴AG=
| 1 |
| 4 |
| ||
| 3 |
点评:本题主要考查线线,线面,面面平行,垂直关系的转化与应用,属中档题.

练习册系列答案
相关题目
 (2013•内江二模)如图,在多面体ABCDEF中,ABCD为菱形,∠ABC=60°,EC⊥面ABCD,FA⊥面ABCD,G为BF的中点,若EG∥面ABCD.
(2013•内江二模)如图,在多面体ABCDEF中,ABCD为菱形,∠ABC=60°,EC⊥面ABCD,FA⊥面ABCD,G为BF的中点,若EG∥面ABCD.