题目内容
8.已知抛物线y2=2px(p>0)的准线经过点(-1,1),则该抛物线焦点坐标为( )| A. | (-1,0) | B. | (1,0) | C. | (0,-1) | D. | (0,1) |
分析 利用抛物线y2=2px(p>0)的准线经过点(-1,1),求得$\frac{p}{2}$=1,即可求出抛物线焦点坐标.
解答 解:∵抛物线y2=2px(p>0)的准线经过点(-1,1),
∴$\frac{p}{2}$=1,
∴该抛物线焦点坐标为(1,0).
故选:B.
点评 本题考查抛物线焦点坐标,考查抛物线的性质,比较基础.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
19.若tanα=$\frac{1}{3}$,tan(α+β)=$\frac{1}{2}$,则tanβ=( )
| A. | $\frac{1}{7}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{6}$ |
16.某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是( )
| A. | 抽签法 | B. | 系统抽样法 | C. | 分层抽样法 | D. | 随机数法 |
3.一辆小客车上有5名座位,其座号为1,2,3,4,5,乘客P1,P2,P3,P4,P5的座位号分别为1,2,3,4,5.他们按照座位号顺序先后上车,乘客P1因身体原因没有坐自己1号座位,这时司机要求余下的乘客按以下规则就坐:如果自己的座位空着,就只能坐自己的座位.如果自己的座位已有乘客就坐,就在这5个座位的剩余空位中选择座位.
(Ⅰ)若乘客P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
(Ⅱ)若乘客P1坐到了2号座位,其他乘客按规则就坐,求乘客P5坐到5号座位的概率.
(Ⅰ)若乘客P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
| 乘客 | P1 | P2 | P3 | P4 | P5 |
| 座位号 | 3 | 2 | 1 | 4 | 5 |
| 3 | 2 | 4 | 5 | 1 | |
| 3 | 2 | 4 | 1 | 5 | |
| 3 | 2 | 5 | 4 | 1 |
20.若集合M={x|-2≤x<2},N={0,1,2},则M∩N=( )
| A. | {0} | B. | {1} | C. | {0,1,2} | D. | {0,1} |
18.阅读如图所示的程序框图,运行相应的程序,则输出i的值为( )
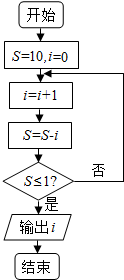

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
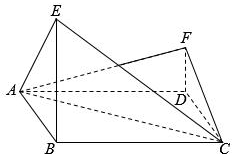 如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.
如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC. 如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,
如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,