题目内容
7.已知直线l的参数方程为$\left\{{\begin{array}{l}{x=-1+t}\\{y=1+t}\end{array}}$(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为${ρ^2}cos2θ=4(ρ>0,\frac{3π}{4}<θ<\frac{5π}{4})$,则直线l与曲线C的交点的极坐标为(2,π).分析 求出直线以及曲线的直角坐标方程,然后求解交点坐标,转化我2极坐标即可.
解答 解:直线l的参数方程为$\left\{{\begin{array}{l}{x=-1+t}\\{y=1+t}\end{array}}$(t为参数),它的直角坐标方程为:x-y+2=0;
曲线C的极坐标方程为${ρ^2}cos2θ=4(ρ>0,\frac{3π}{4}<θ<\frac{5π}{4})$,
可得它的直角坐标方程为:x2-y2=4,x<0.
由$\left\{\begin{array}{l}x-y+2=0\\{x}^{2}-{y}^{2}=4\end{array}\right.$,可得x=-2,y=0,
交点坐标为(-2,0),
它的极坐标为(2,π).
故答案为:(2,π).
点评 本题考查曲线的极坐标方程直线的参数方程与普通方程的互化,基本知识的考查.

练习册系列答案
相关题目
15.已知集合A={1,2,3},B={2,3},则( )
| A. | A=B | B. | A∩B=∅ | C. | A$\stackrel{?}{≠}$B | D. | B$\stackrel{?}{≠}$A |
2.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点为F,右顶点为A,过F作AF的垂线与双曲线交于B,C两点,过B,C分别作AC,AB的垂线,两垂线交于点D.若D到直线BC的距离小于a+$\sqrt{{a^2}+{b^2}}$,则该双曲线的渐近线斜率的取值范围是( )
| A. | (-1,0)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-$\sqrt{2}$,0)∪(0,$\sqrt{2}$) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
19.若tanα=$\frac{1}{3}$,tan(α+β)=$\frac{1}{2}$,则tanβ=( )
| A. | $\frac{1}{7}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{6}$ |
16.某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是( )
| A. | 抽签法 | B. | 系统抽样法 | C. | 分层抽样法 | D. | 随机数法 |
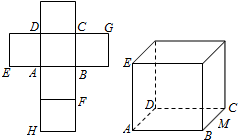 一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M、GH的中点为N.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M、GH的中点为N. 如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.
如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC. 如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,
如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,