题目内容
【题目】已知椭圆C:![]() (
(![]() )的两焦点与短轴两端点围成面积为12的正方形.
)的两焦点与短轴两端点围成面积为12的正方形.
(1)求椭圆C的标准方程;
(2)我们称圆心在椭圆上运动,半径为![]() 的圆是椭圆的“卫星圆”.过原点O作椭圆C的“卫星圆”的两条切线,分别交椭圆C于A、B两点,若直线
的圆是椭圆的“卫星圆”.过原点O作椭圆C的“卫星圆”的两条切线,分别交椭圆C于A、B两点,若直线![]() 、
、![]() 的斜率为
的斜率为![]() 、
、![]() ,当
,当![]() 时,求此时“卫星圆”的个数.
时,求此时“卫星圆”的个数.
【答案】(1)![]() ;(2)8个.
;(2)8个.
【解析】
(1)由条件可得![]() ,解出来即可;
,解出来即可;
(2) 设“卫星圆”的圆心为![]() ,由定义可得“卫星圆”的标准方程为
,由定义可得“卫星圆”的标准方程为![]() ,求其圆心到直线
,求其圆心到直线![]() ,直线
,直线![]() 的距离,整理可转化为
的距离,整理可转化为![]() 、
、![]() 是方程
是方程![]() 的两个不相等的实数根,则
的两个不相等的实数根,则![]() ,再加上
,再加上![]() ,
,![]() ,解方程即可.
,解方程即可.
(1)∵椭圆C的两焦点与短轴两端点围成面积为12的正方形,
∴由椭圆的定义和正方形的性质,可得![]() ,
,
解得![]() .
.
又![]()
∴椭圆C的标准方程为![]() .
.
(2)设“卫星圆”的圆心为![]() .
.
由“卫星圆”的定义,可得“卫星圆”的半径为![]() .
.
∴“卫星圆”的标准方程为![]() .
.
∵直线![]() :
:![]() 与“卫星圆”相切,
与“卫星圆”相切,
则由点到直线的距离公式可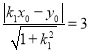 ,
,
化简得![]() .
.
同理可得![]() .
.
∴![]() 、
、![]() 是方程
是方程![]() 的两个不相等的实数根,
的两个不相等的实数根,
∴![]() ,由
,由![]() ,得
,得![]() ,
,
将![]() 代入得
代入得![]() ,
,![]() .
.
又∵“卫星圆”的圆心![]() 在椭圆C上,
在椭圆C上,
∴代入椭圆方程![]() 中,可得
中,可得![]() .
.
解得![]() ,
,
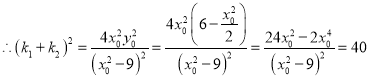 .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
∴满足条件的点![]() 共8个,
共8个,
∴这样“卫星圆”存在8个.

练习册系列答案
相关题目
