题目内容
已知函数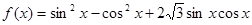 。求函数
。求函数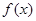 的单调递增区间和最小值;
的单调递增区间和最小值;
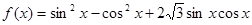 。求函数
。求函数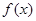 的单调递增区间和最小值;
的单调递增区间和最小值;
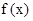 的最小值为-2
的最小值为-2第一问中利用三角函数的二倍角公式求解运算得到性质。利用二倍角公式求解
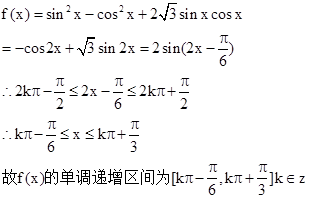
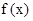 的最小值为-2
的最小值为-2
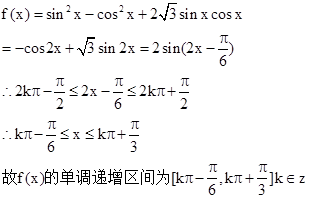
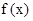 的最小值为-2
的最小值为-2
练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
题目内容
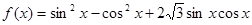 。求函数
。求函数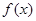 的单调递增区间和最小值;
的单调递增区间和最小值;
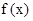 的最小值为-2
的最小值为-2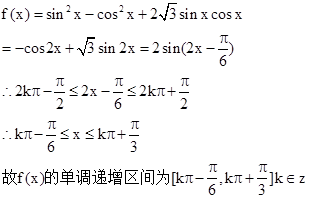
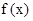 的最小值为-2
的最小值为-2
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案