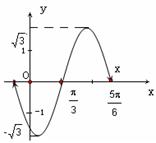
题目内容
设函数f (x)=2cosx (cosx+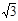 sinx)-1, x∈R.
sinx)-1, x∈R.
(1)求f (x)的最小正周期T及单调递增区间;
(2)在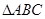 中,
中,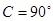 ,求f (A)的取值范围.
,求f (A)的取值范围.
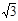 sinx)-1, x∈R.
sinx)-1, x∈R.(1)求f (x)的最小正周期T及单调递增区间;
(2)在
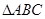 中,
中,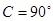 ,求f (A)的取值范围.
,求f (A)的取值范围.(1)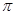 ,单调增区间为
,单调增区间为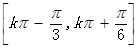 ,
,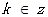 ;(2)
;(2)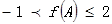 .
.
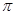 ,单调增区间为
,单调增区间为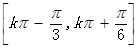 ,
,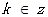 ;(2)
;(2)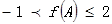 .
.第一问首先化为单一三角函数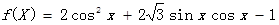 =
=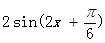 ,然后利用周期公式和正弦函数的单调区间求解得到。由
,然后利用周期公式和正弦函数的单调区间求解得到。由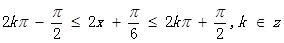 得
得
第二问中,由已知得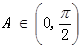 ,
,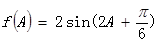 ,因此得到
,因此得到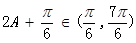
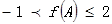 即为所求。
即为所求。
解: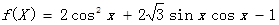
=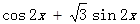
=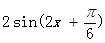 ……………3分
……………3分
(1) T=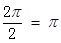 ……………………4分
……………………4分
由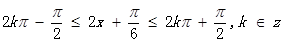 得
得
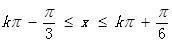
故函数的单调增区间为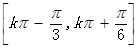 ,
, ………7分
………7分
(2) 由已知得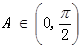 ,
,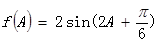
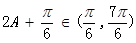
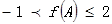 ……………………12分
……………………12分
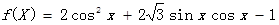 =
=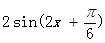 ,然后利用周期公式和正弦函数的单调区间求解得到。由
,然后利用周期公式和正弦函数的单调区间求解得到。由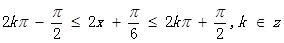 得
得第二问中,由已知得
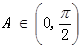 ,
,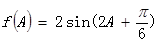 ,因此得到
,因此得到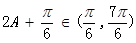
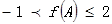 即为所求。
即为所求。解:
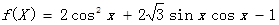
=
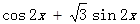
=
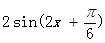 ……………3分
……………3分(1) T=
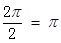 ……………………4分
……………………4分由
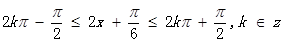 得
得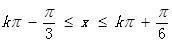
故函数的单调增区间为
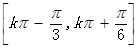 ,
,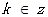 ………7分
………7分(2) 由已知得
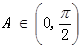 ,
,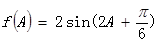
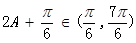
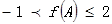 ……………………12分
……………………12分
练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
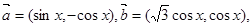 设函数
设函数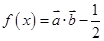 ;
; 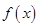 的单调递增区间;
的单调递增区间;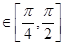 求函数
求函数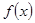 的最值及对应的x的值;
的最值及对应的x的值;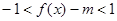 在x
在x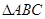 的三个内角
的三个内角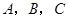 依次成等差数列.
依次成等差数列.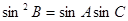 ,试判断
,试判断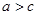 ,求
,求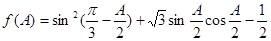
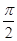 ,j=
,j=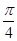
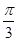 ,j=
,j=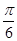
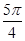
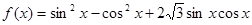 。求函数
。求函数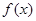 的单调递增区间和最小值;
的单调递增区间和最小值; 在区间
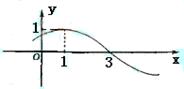
在区间 的简图是( )
的简图是( )

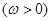 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为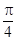 .
.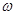 值;(2)若
值;(2)若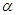 是第四象限角,
是第四象限角,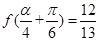 ,求
,求 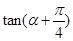 的值
的值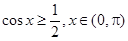 ,且
,且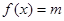 有且仅有一个实根,求实数
有且仅有一个实根,求实数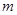 的值.
的值.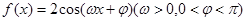 的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移
的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移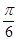 个单位后得到一个最小正周期为2
个单位后得到一个最小正周期为2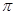 的奇函数
的奇函数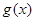 .
.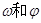 的值;
的值;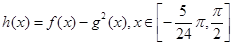 的单调区间和最值.
的单调区间和最值.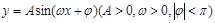 的部分图象, 则
的部分图象, 则