题目内容
已知函数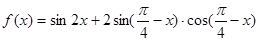
(1) 求函数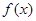 的最小正周期; (2) 求函数
的最小正周期; (2) 求函数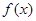 在区间
在区间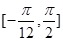 上的值域;
上的值域;
(3)借助”五点作图法”画出函数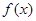 在
在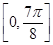 上的简图,并且依图写出函数
上的简图,并且依图写出函数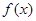 在
在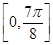 上的递增区间.
上的递增区间.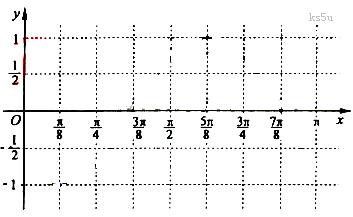
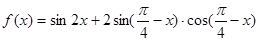
(1) 求函数
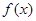 的最小正周期; (2) 求函数
的最小正周期; (2) 求函数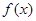 在区间
在区间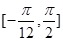 上的值域;
上的值域;(3)借助”五点作图法”画出函数
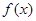 在
在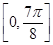 上的简图,并且依图写出函数
上的简图,并且依图写出函数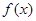 在
在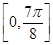 上的递增区间.
上的递增区间.
(1) 周期T = 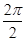 = p (2) [-1,
= p (2) [-1,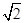 ] (3)
] (3)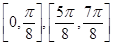
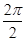 = p (2) [-1,
= p (2) [-1,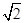 ] (3)
] (3)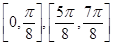
(1)(2)解本小题的关键是根据两角和与差的诱导公式化为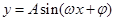 形式再求出周期,单调性,最值等.
形式再求出周期,单调性,最值等.
(3)用五点法作图,要先令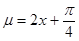 ,分别取
,分别取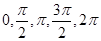 算出对应的x的值,以及y值,然后描点,连线即可成图
算出对应的x的值,以及y值,然后描点,连线即可成图
(1) ∵ f (x) =" sin" 2x + sin (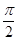 -2x) =" sin" 2x + cos 2x
-2x) =" sin" 2x + cos 2x
=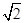 (
(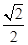 sin 2x +
sin 2x + 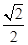 cos 2x) =
cos 2x) = 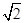 (sin 2x cos
(sin 2x cos 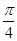 + cos 2x sin
+ cos 2x sin 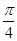 )=
)= 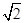 sin (2x +
sin (2x + 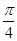 )
)
∴ 周期T =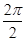 = p …………………4分
= p …………………4分
(2) ∵x∈[-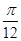 ,
,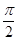 ] Þ 2x +
] Þ 2x + 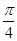 ∈[
∈[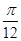 ,
,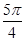 ]∴ 当 2x +
]∴ 当 2x + 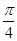 =
= 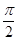 时,
时,
f (x) 取最大值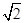 sin
sin 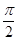 =
= 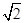 ;………………………………………………5分
;………………………………………………5分
当 2x +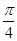 =
= 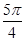 时,f (x) 取最小值
时,f (x) 取最小值 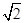 sin
sin 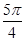 = -1…………………………7分
= -1…………………………7分
∴ 函数 f (x) 在区间 [-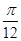 ,
,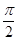 ] 上的值域为 [-1,
] 上的值域为 [-1,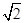 ] ……………………8分
] ……………………8分
(3)列表
……………………………………………………10分
图象略,注意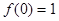 ……………………………12分
……………………………12分
函数在区间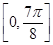 上的单调递增区间是
上的单调递增区间是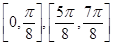
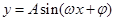 形式再求出周期,单调性,最值等.
形式再求出周期,单调性,最值等.(3)用五点法作图,要先令
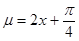 ,分别取
,分别取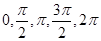 算出对应的x的值,以及y值,然后描点,连线即可成图
算出对应的x的值,以及y值,然后描点,连线即可成图(1) ∵ f (x) =" sin" 2x + sin (
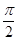 -2x) =" sin" 2x + cos 2x
-2x) =" sin" 2x + cos 2x=
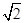 (
(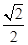 sin 2x +
sin 2x + 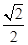 cos 2x) =
cos 2x) = 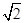 (sin 2x cos
(sin 2x cos 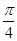 + cos 2x sin
+ cos 2x sin 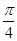 )=
)= 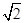 sin (2x +
sin (2x + 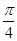 )
)∴ 周期T =
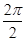 = p …………………4分
= p …………………4分(2) ∵x∈[-
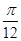 ,
,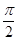 ] Þ 2x +
] Þ 2x + 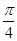 ∈[
∈[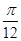 ,
,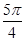 ]∴ 当 2x +
]∴ 当 2x + 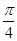 =
= 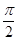 时,
时,f (x) 取最大值
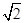 sin
sin 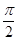 =
= 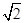 ;………………………………………………5分
;………………………………………………5分当 2x +
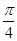 =
= 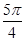 时,f (x) 取最小值
时,f (x) 取最小值 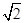 sin
sin 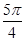 = -1…………………………7分
= -1…………………………7分∴ 函数 f (x) 在区间 [-
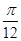 ,
,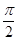 ] 上的值域为 [-1,
] 上的值域为 [-1,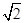 ] ……………………8分
] ……………………8分(3)列表
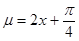 |  | 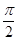 | 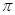 | 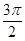 | 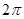 |
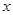 | 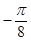 | 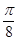 | 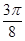 | 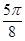 | 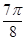 |
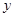 |  | 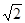 |  | 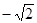 |  |
图象略,注意
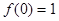 ……………………………12分
……………………………12分函数在区间
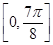 上的单调递增区间是
上的单调递增区间是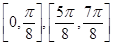

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
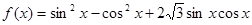 。求函数
。求函数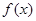 的单调递增区间和最小值;
的单调递增区间和最小值;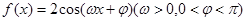 的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移
的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移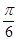 个单位后得到一个最小正周期为2
个单位后得到一个最小正周期为2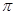 的奇函数
的奇函数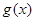 .
.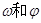 的值;
的值;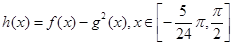 的单调区间和最值.
的单调区间和最值.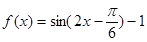 ;
; 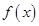 的单调递增区间;
的单调递增区间; 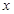
 求函数
求函数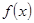 的最值及对应的
的最值及对应的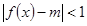 在
在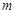 的取值范围.
的取值范围. (
( ,
, ),且函数
),且函数 的最小正周期为
的最小正周期为 .
. 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为 ,若
,若 =1,
=1, ,且
,且 ,求边长
,求边长 .
.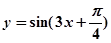 的图象可由函数
的图象可由函数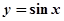 的图象怎样变换而来?( )
的图象怎样变换而来?( ) ,再纵坐标不变,横坐标缩短为原来的
,再纵坐标不变,横坐标缩短为原来的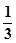
 ,再纵坐标不变,横坐标缩短为原来的
,再纵坐标不变,横坐标缩短为原来的 ( )
( )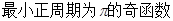



 )
)  )
)
 的最大值和最小值分别为
的最大值和最小值分别为 ,则
,则